SPI 『仕事算・水槽算』 ～練習問題と解き方を徹底解説！～

仕事算・水槽算の練習問題を解く前にまずは、以下の内容をしっかりと熟読し、理解してから解くようにしてください。そうすることで、試験本番でもスムーズに解けるようになると思います。

SPI 仕事算・水槽算の問題の解き方

SPIの仕事算・水槽算の問題を解く上で最も重要なことは、『全体の仕事量を１と仮定する』ことです。正確に言うと、『１』である必要はないのですが、何らかの数値を仮定することが大切です。

『えっ！？そんな勝手に仕事量を設定してもいいの？』と思う人もいるかもしれませんが、構いません。

例えば、Ａさんが全てを終えるのに１０日間かかる仕事があったとします。そうすると、全体の仕事量を１とした場合、Ａさんの１日の仕事量は１１０となります。

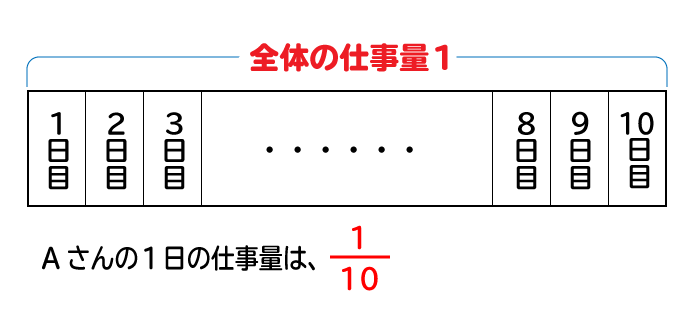
もし、全体の仕事量を１ではなく１０と仮定した場合はどうなるでしょうか？

Ａさんが全てを終えるのに１０日間かかる仕事量を１０とした場合、Ａさんの１日の仕事量は１となります。

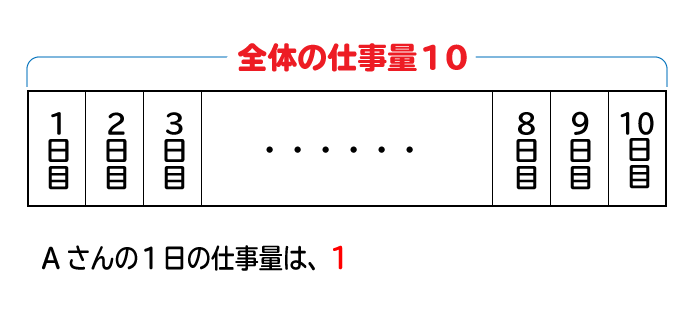
全体の仕事量を１とした場合、Ａさんの１日の仕事量は１１０、全体の仕事量を１０とした場合のＡさんの１日の仕事量は１となり、一見異なるように見えますが全体の作業量に対して１日の作業量は実は双方とも１１０なのです。

要は、全体の作業量を仮定する数値はいくつに設定しても同じということです。いくつに設定するかは、その都度、計算しやすい数値に設定すれば構いません。

例えば、上記の例であれば全体の作業量を１０と仮定した方がＡさんの１日の作業量を分数を使わなくて表さなくて済むので計算が簡単になりますよね。

仕事算の簡単な練習問題

全体の仕事量を1と仮定します。

Ａ君はこの仕事量1を終えるのに20日かかるので、1日の作業量は120となります。

次にＢ君は仕事量1を終えるのに30日かかるので、1日の作業量は130となります。

よって、Ａ君とＢ君が一緒に1日作業した場合、1日に進む仕事量は次の通り。

Ａ君とＢ君が一緒に作業した場合の1日の仕事量
120＋130
＝360＋260
＝560
＝112

求めたいのは、すべての仕事を終えるのに何日かかるかですよね？その日数をＮ日と仮定します。1日に進む仕事量は112です。これをＮ日繰り返して、全体の仕事量1となればいいわけです。よって、以下の式が成り立ちます。

112×Ｎ＝1

この式を計算すると、仕事を終えるのにかかる日数Ｎが求まります。

112×Ｎ＝1
Ｎ＝1×12
Ｎ＝12

よって、すべての仕事を終えるのにかかる日数は12日

全体の仕事量を1以外に設定した場合の解き方

全体の仕事量を1以外に設定する場合の解き方です。設定する数値は、各々の仕事にかかる日数を最小公倍数を設定すると計算が楽になることが多いです。今回の練習問題であれば、各々の仕事にかかる日数が20日と30日となっています。よって、20と30の最小公倍数である60を全体の仕事量として設定すると計算が楽になります。

全体の仕事量を60と仮定します。

Ａ君はこの仕事量60を終えるのに20日かかるので、1日の作業量は3となります。

次にＢ君は仕事量60を終えるのに30日かかるので、1日の作業量は2となります。

よって、Ａ君とＢ君が一緒に1日作業した場合、1日に進む仕事量は3+2＝5だと分かります。

Ａ君とＢ君が一緒に作業した場合の1日の仕事量は、5なので、全体の仕事量60を終えるのにかかる日数は次の通り。

5×Ｎ＝60
Ｎ＝12

よって、すべての仕事を終えるのにかかる日数は12日

どうでしょうか？
分数の計算が一切発生せず簡単ですよね？
是非、マスターして短時間で問題が正確に解けるように繰り返し練習してください。