
n進法の練習問題を解く前にまずは、以下の内容をしっかりと熟読し、理解してから解くようにしてください。そうすることで、試験本番でもスムーズに解けるようになると思います。
SPI n進法の問題の解き方
n進法の問題は最低限以下の二種類の変換方法を知っていればどんな問題でも解くことができます。
(1)10進数からn進数への変換
(2)n進数から10進数への変換
しかし、SPIは如何に早くかつ、正確に解くかが重要になってくるため、上記二種類に加え、以下の変換方法も知っておくと良いかと思います。
(3)n進数からn進数への変換
例えば、(1)と(2)の変換方法しか知らないと、2進法から8進法への変換問題が出題された場合、(2)の変換方法で一度、2進法から10進法へ変換した後、(1)の方法で10進法から8進法へ変換する必要が出てきます。そのため、時間がかかるだけではなく、計算ミスをするリスクも高くなってしまいます。
知っておくべき3種類の変換方法
このページで上記3種類の変換方法を詳しく解説しているので、練習問題をする前に必ず一読し、理解するようにしてください。
10進数からn進数への変換方法
10進数からn進数への変換は他にもやり方はあるのですが、確実で早いのがやはり一般的な10進数の数をnで割れなくなるまで割っていくやり方です。「割れなくなる」と言うと、色々と語弊があるのですが、正確に言うと、『nで割った時の商がnより小さくなるまで割る』です。
10進数から2進数に変換する場合であれば、10進数の数を2で割った時の商が0もしくは1になるまで割るということです。
では、10進数の97を、『2進数』、『8進数』、『16進数』にそれぞれ変換する例をやってます。
10進数の97を、『2進数』に変換する
10進数からn進数への変換は『10進数の数をnで割れなくなるまで割っていく』でしたよね。よって、10進数の97を2で割れなくなるまで割っていきます。また、その際、下図のように右横に割った余りを記載しておきます。
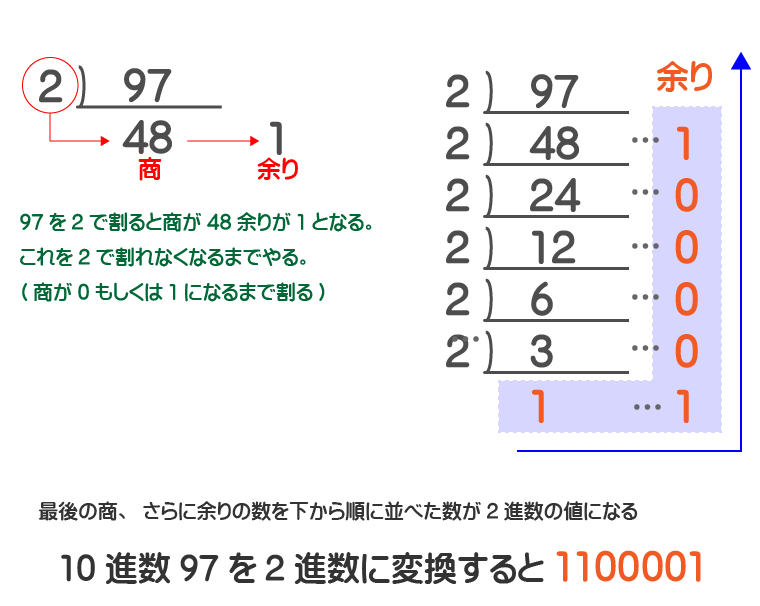
10進数の97を、『8進数』に変換する
10進数からn進数への変換は『10進数の数をnで割れなくなるまで割っていく』なので、今度はn=8となります。よって、10進数の97を8で割れなくなるまで割っていきます。
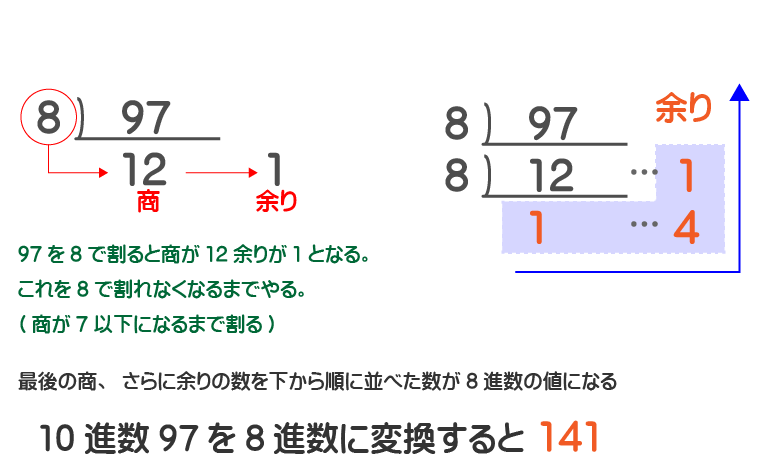
10進数の97を、『16進数』に変換する
10進数からn進数への変換は『10進数の数をnで割れなくなるまで割っていく』なので、今度はn=16となります。よって、10進数の97を16で割れなくなるまで割っていきます。
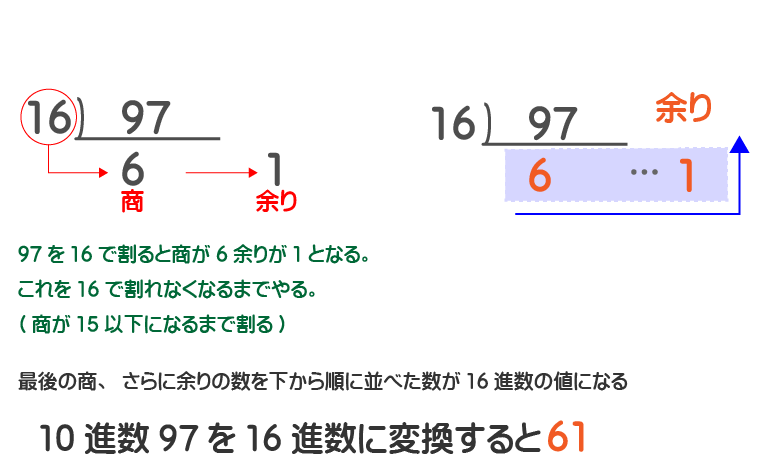
補足事項
- これらのやり方は、10進数を3進数や、7進数に変換する場合でも同じで、n進数のnで割っていくことで算出できます。
n進数から10進数への変換方法
n進数を10進数に変換する場合は、1桁目(右端の桁)から順にn⁰、n¹、n²・・・を順番に掛けていったものを合計することで算出できます。
では、2進数、8進数、16進数の数を10進数に変換する例を解説していきます。
2進数の1100001を、『10進数』に変換する
n進数を10進数に変換する場合は、『1桁目(右端の桁)から順にn⁰、n¹、n²・・・を順番に掛けていく』でしたよね。よって、2⁰、2¹、2²・・・を2進数の1桁目から順にかけていきます。
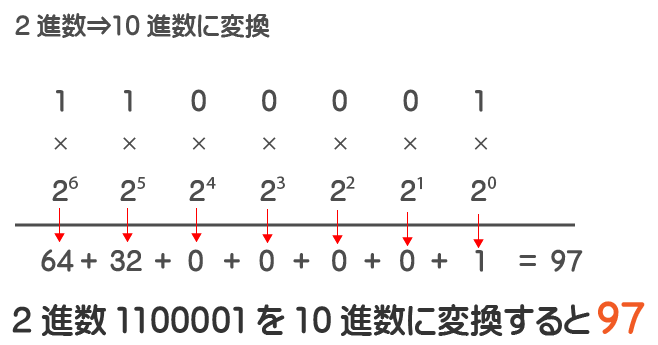
8進数の141を、『10進数』に変換する
n進数を10進数に変換する場合は、『1桁目(右端の桁)から順にn⁰、n¹、n²・・・を順番に掛けていく』なので、8⁰、8¹、8²・・・を8進数の1桁目から順にかけていきます。

16進数の61を、『10進数』に変換する
n進数を10進数に変換する場合は、『1桁目(右端の桁)から順にn⁰、n¹、n²・・・を順番に掛けていく』なので、16⁰、16¹を16進数の1桁目から順にかけていきます。

n進数から10進数への変換方法【別解-最速の解き方】
n進数から10進数へ変換する場合は別の解き方があります。慣れるとこちらの方が簡単で早いので、SPIなどスピードが要求される人は是非、覚えておいてください。
その解き方は次の3ステップで行います。
n進数から10進数への変換手順
- n進数の1桁目を除く各桁にnを掛ける(この時点では掛け算の式を書くだけで計算はまだしない)
- 各桁を足し算する(この時点では足し算の式を書くだけで計算はまだしない)
- 左から順に計算していく
まず、方法はn進数の1桁目を除く各桁にnを掛けます。
例えば、2進数『111101』を10進数に変換したい場合であれば、次のような流れになります。
①n進数の1桁目を除く各桁にnを掛ける(この時点では掛け算の式を書くだけで計算はまだしない)
1×2 1×2 1×2 1×2 0×2 1
②各桁を足し算する(この時点では足し算の式を書くだけで計算はまだしない)
1×2+1×2+1×2+1×2+0×2+1
③左から順に計算していく
通常の計算は足し算より掛け算を優先的に計算するのですが、ここでは優先度関係なく左から順番に計算していきます。
今回の例であれば、次の様になります。
①1x2=2
②2+1=3
③3x2=6
④6+1=7
⑤7x2=14
⑥14+1=15
⑦15x2=30
⑧30+0=30
⑨30x2=60
⑩60+1=61
答え61
先程の例で2進数(1100001)、8進数(141)、16進数(61)を10進数に変換する場合は、次のようになります。実に簡単ですね。

n進数からn進数への変換方法
SPIなど計算スピードが求められる場合は、このn進数からn進数に変換する方法も是非、覚えておくようにしてください。
ただし、このn進数からn進数への変換方法は、n進数が2進数、8進数、16進数のいずれかの場合しか利用できません。
例えば、2進数から5進数への変換や3進数から7進数への変換には利用できません。これらの変換をしたい場合は、一旦、10進数に変換した後、目的のn進数に変換する必要があります。(例:3進数⇒10進数⇒7進数)
2進数から8進数に変換する場合
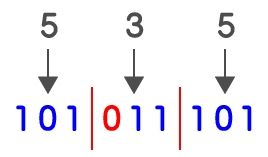
2進数を下1桁から3桁ずつで区切り線をいれていきます。2進数11101101の場合であれば、下記のようになります。

3桁ずつ区切っていく上で、桁が足りない場合は上記のように0を補充して3桁にします。次にこの区切った3桁ごとに8進数に置き換えます。
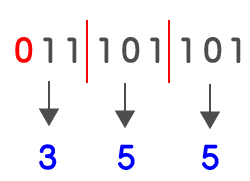
よって、2進数11101101を8進数に置き換えると、355となります。これをさらに素早く解くために『2進数と10進数と16進数の対応表』程度は頭に入れて置き、瞬時に出てくるようにしておきましょう。
2進数から16進数に変換する場合
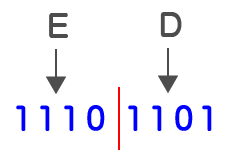
2進数から8進数に変換する場合は、3桁ごとに分けましたが、16進数の場合は4桁ごとに分けます。2進数11101101の場合であれば、次のようになります。
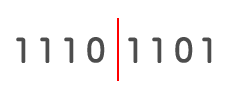
今度は丁度4桁ごとに分割できたので、0の補充は必要ありません。引き続き分割した4桁ごとに16進数に変換します。
「1110」は16進数になおすと「E」、「1101」を16進数になおすと「D」になります。
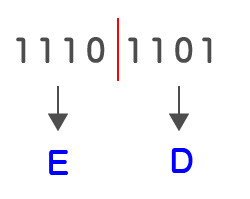
よって、2進数11101101を16進数に置き換えると、EDとなります。
8進数から2進数に変換する場合
これは、2進数から8進数へ変換する方法の逆の手順になります。8進数355を2進数に変換する場合、各桁を2進数に置き換えます。
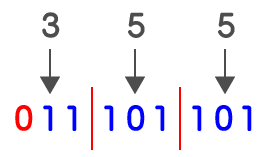
2進数に置き換えた際に3桁にならない場合は0を補充して3桁にすることを忘れないようにしてください。上記のような場合は、一番左が0なので補充せず省略も可能ですが、下記のような場合、0の補充を忘れると誤った解答になってしまいます。
16進数から2進数に変換する場合
2進数から16進数へ変換する方法の逆の手順になります。16進数EDを2進数に変換する場合、各桁を2進数に置き換えます。2進数に置き換えた際に4桁にならない場合は0を補充して4桁にして下さい。
どうでしょう。これらの変換方法を一通り覚えておけばn進法の問題は全て解くことができます。
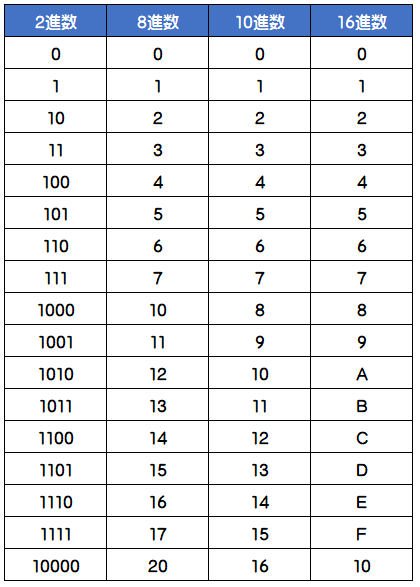
2進数、8進数、10進数、16進数の対応表
最低限、下記の対応表は頭に入れて置き、頭の中で瞬時に変換できるようにしておきましょう。
何度も記載していますが、SPIは解き方を知っているだけでは不十分です。いかに早くかつ、正確に解けるかが重要です。
ゲームのタイムアタックのような感覚で、何度も繰り返し解き、タイムを縮めていってください。










