SPI練習問題-問14(推論・論証)

SPI練習問題-問14(推論・論証)

推論(順番)に関する問題。次の設問1、設問2を解答せよ。

5つの野球チームＰ、Ｑ、Ｒ、Ｓ、Ｔで毎年、野球大会が行われている。今年の結果について次のことが分かっている。

1. Ｐは昨年と比べて順位が3つ下がった
2. 昨年Ｑは4位だった
3. 昨年も今年もＳの順位はＴの順位の1つ下だった
4. 昨年と今年で順位が同じチームは一つもなかった

[設問１]昨年Ｔは何位だったか？

[設問２]次の推論ア、イ、ウの内、正しいものはどれか？Ａ～Ｈの中から1つ選びなさい。

• ア：今年5位になったのはＲだ
• イ：Ｑは昨年も今年も3位以上になっていない
• ウ：今年、ＳはＰより上位だった

解答と解説

『推論・論証』の問題の解き方や、使う公式に関しては『SPI 推論・論証 ～練習問題と解き方を徹底解説！～』のページで詳しく解説しています。解き方が分からない方は、まず、そちらのページを一読してください。

設問１の解答と解説：

ⅰ～ⅳの分かっていることを順に確認していきます。頭の中で考えるのではなく、必ず分かっている点を図式化、数式化するようにしてください。

ⅰ：Ｐは昨年と比べて順位が3つ下がった

昨年と比べて順位が3つ下がったということなので、Ｐの昨年の順位は1位もしくは2位だと分かります。もし、昨年が3位以下だった場合、今年の順位が6位以下とあり得ない順位になる。

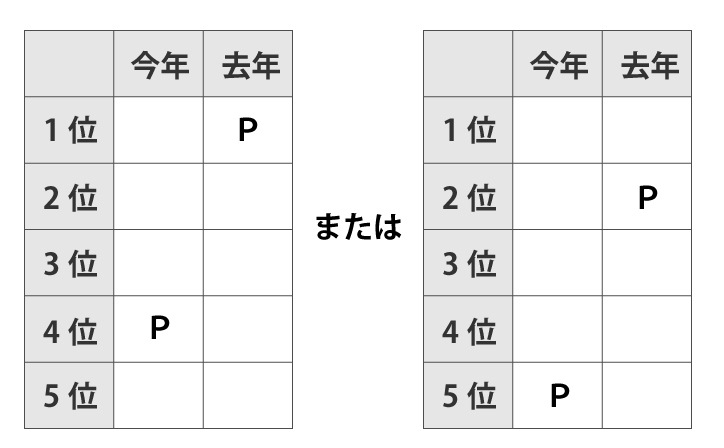
ⅱ：昨年Ｑは4位だった

Ｑは昨年4位だったので、分かっている点を表に追加すると下表になります。

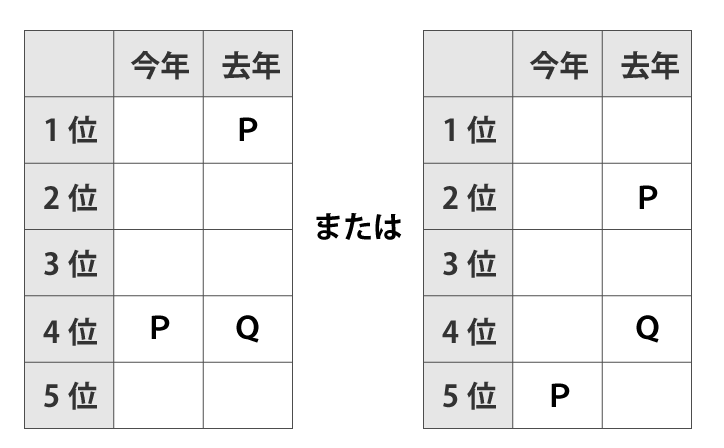
ⅲ：昨年も今年もＳの順位はＴの順位の1つ下だった

昨年も今年もＳの順位はＴの順位の1つ下だったということなので、Ｔ、Ｓと連続した順位になるが、下表右の去年の順位欄は連続した空きが、これまでの確認で既に無くなっています。よって、下表左のみに絞られます。

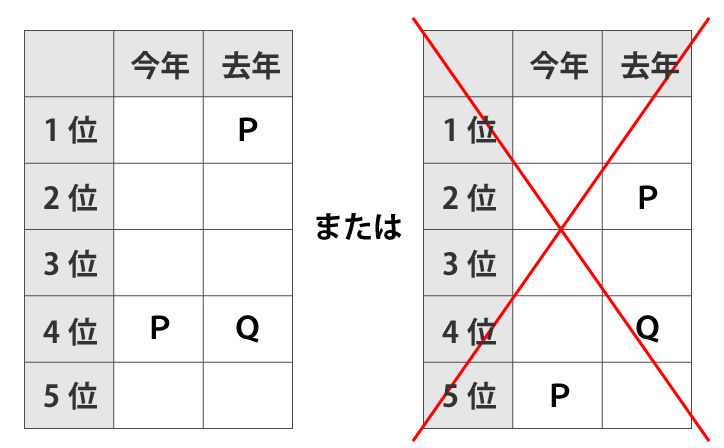
そうすると、Ｔは昨年2位、Ｓは3位が確定し、残るＲが5位と確定します。また、今年の順位はＴが1位でＳが2位もしくは、Ｔが2位でＳが3位となります。

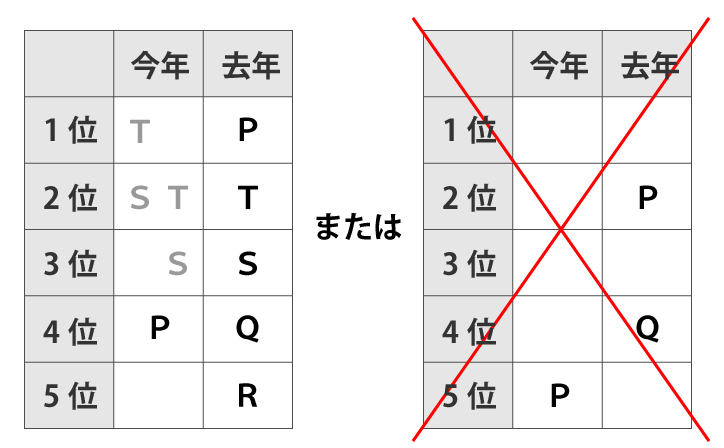
ⅳ：昨年と今年で順位が同じチームは一つもなかった

昨年と今年で順位が同じチームは一つもなかったということなので、今年のＴは1位、Ｓは2位、Ｒは3位が確定します。そうすると、残るＱは5位になります。

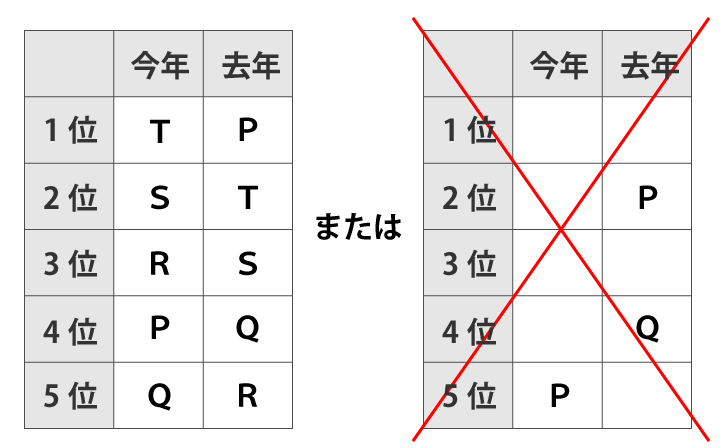
よって、設問１のＴの昨年の順位は2位となる。

解答：Ｂ

設問２の解答と解説：

設問１で各チームの順位は出ているので、ア～ウの正誤を確認していきます。

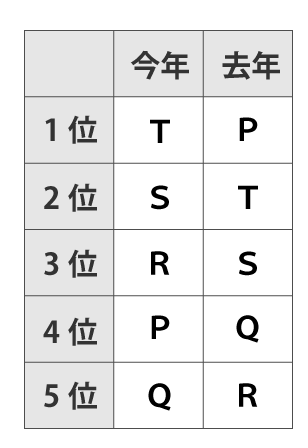
ア：今年5位になったのはＲだ

今年5位になったのはＱなので誤り

イ：Ｑは昨年も今年も3位以上になっていない

Ｑは昨年4位、今年5位なので正しい

ウ：今年、ＳはＰより上位だった

今年のＳは2位でＰは4位なので正しい

よって、正しいのはイとウのＦ

解答：Ｆ