SPI練習問題-問1(n進法)

SPI練習問題-問1(n進法)

ｎ進法に関する次の問題に答えなさい。

[設問１]１０進法の５７は２進法ではいくつか？

[設問２]５進法の３２４は１０進法ではいくつか？

[設問３]３進法の１０２＋１２２は３進法ではいくつか？

解答と解説

使用する公式：
ｎ進法の解き方に関しては、『SPI ｎ進法 ～練習問題と徹底解説！～』のページで詳しく解説しているので、参考にしてください。早く解く方法なども紹介しています。

設問１の解答と解説：

10進数から2進数の変換は、10進数の数を2で割った時の商が0もしくは1になるまで割り続け、その時の最後の商、さらに余りの数を下から順に並べた数が2進数の値になります。

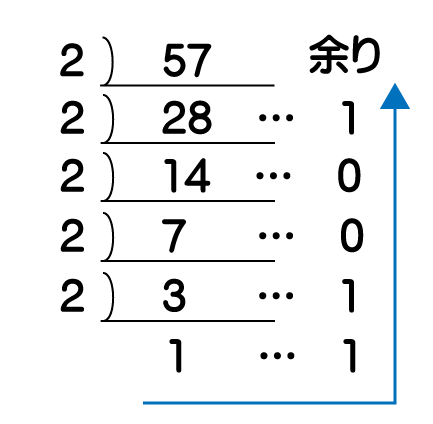
よって、解答は、111001

解答：Ｅ

設問２の解答と解説：

ｎ進数から10進数への変換方法は『SPI ｎ進法 ～練習問題と徹底解説！～』のページでも詳しく解説していますが、、2通りあります。最も一般的な解き方は、ｎ進数の一桁目から順にｎ⁰、ｎ¹、ｎ²・・・を掛けていく方法です。

5進数に変換なので、ｎ＝5になります。よって、10進数の324を5進数に変換すると次の通り。

　(3ｘ5²)＋(2ｘ5¹)＋(4ｘ5⁰)
＝ (3ｘ25)＋(2ｘ5)＋(4ｘ1)
＝ 89

別の解き方

もう1つの解き方は、1桁目を除き各桁にｎを掛けて横の桁と足していく。ただし、注意点として本来の計算なら足し算より掛け算を優先にすべきですが、この方法で解く場合は、優先度は関係なしに左から順番に計算していきます。

まず、324の各桁に5を掛けて隣のけたと足し算します。式としては次のようになります。

　3ｘ5＋2ｘ5＋4＝

これを左から順番に計算していくと下記のようになります。

　3ｘ5＋2ｘ5＋4
＝15＋2ｘ5＋4
＝17ｘ5＋4
＝85＋4
＝89

解答：Ｅ

設問３の解答と解説：

この問題は3進法の足し算になります。一旦10進法に置き換えて計算する方法もありますが、時間を節安するためにも3進法のままで計算できるりょうにしましょう。

　１０２
＋１２２
－－－－－
　２２４

普通に計算すると224となってしまいます。しかし、これは3進法なので表現できる数値は0、1、2の3つのみです。3以上の数値は桁上がりが発生します。
よって、桁上がりを考慮すると次のようになります。

　１０２
＋１２２
－－－－－
１００１

どうしても桁上がりの計算がややこしく感じる方は、10進数に置き換えて計算する方が早い場合もあります。しかし、その場合は計算後、再度3進数に戻すのを忘れないようにして下さい。ひっかけで、10進数で計算した結果が解答群に入っている場合などもあります。

解答：Ｄ