SPI練習問題-問2(確率)
確率の問題。
[設問1]3人で同時にじゃんけんをする。少なくとも2人が同じ手を出す確率はいくらか?
[設問2]箱の中に赤玉5つと白玉4つが入っている。一度に二つ取り出したとき、すべて白玉である確率はいくらか?
解答と解説
『確率』の問題の解き方や、使う公式に関しては『SPI 確率 ~練習問題と解き方を徹底解説!~』のページで詳しく解説しています。解き方が分からない方は、まず、そちらのページを一読してください。
設問1の解答と解説:
各々は、グー、チョキ、パーの3通りの出し方があります。よって、3人がじゃんけんをした場合の全組合せパターン数は、
全組合せパターン数
=3×3×3
=27パターン
次に少なくとも2人が同じ手を出すということは、2人が同じ手を出す、もしくは3人とも同じ手を出すという事である。ようは、全員がバラバラの手を出すパターン以外ということと同じである。
全員がバラバラの手を出すパターンは、G(グー)、C(チョキ)、P(パー)としたとき、
G C P
G P C
C G P
C P G
P G C
P C G
上記の6通りだけになる。よって、全27パターン中、6通りが全員バラバラの手を出すパターンなので、21パターン(27-6=21)が、少なくとも2人が同じ手を出すパターン数となる。これを公式①に代入すると、求めたい確率が出る。
少なくとも2人が同じ手を出す確率 = 21/27 = 7/9
解答:7/9
設問2の解答と解説:
確率を求めるためには、公式①で分かる通り、全パターン(組合せ)数と、その事象が起こりうるパターン数を出す必要がある。
まずは、赤玉5つ、白玉4つの計9つの球がある箱の中から、2つを取り出したときの全組み合わせの数を求める。組み合わせ数を求める場合は、次の公式を利用する。

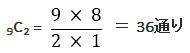
よって、全組合せ数は、36種類あることがわかる。次に、白玉4つから2つを取り出す組み合わせ数は、下記の計算より6組だと分かる。
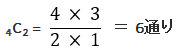
よって、求める確率
=6/36
=1/6
解答:1/6




