SPI 『グラフの領域』 ~練習問題と解き方を徹底解説!~

グラフの領域の練習問題を解く前にまずは、以下の内容をしっかりと熟読し、理解してから解くようにしてください。そうすることで、試験本番でもスムーズに解けるようになると思います。
SPI グラフの領域の問題の解き方
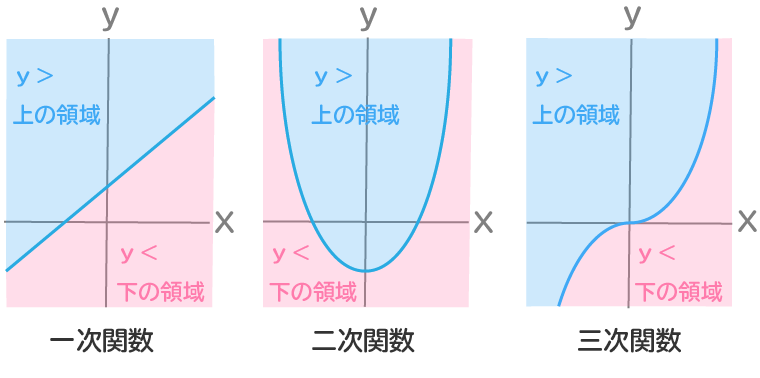
解き方のポイント
- 不等式が『y>』の時は、グラフより上の水色の領域を表します。
- 不等式が『y<』の時は、グラフより下のピンク色の領域を表します。
- 『y=』の時は、グラフの線上を表します。
- 不等式が『y≧』の時は、グラフの線上も含む水色の領域を表します。
- 不等式が『y≦』の時は、グラフの線上も含むピンク色の領域を表します。
SPIのグラフの領域の問題は、1つのグラフが単体で出題されることは少なく、複数のグラフを組み合わせた問題が出題されます。
よって、複数のグラフが重なった場合の指し示す領域が分かるようにしておきましょう。
二つのグラフの重なる領域
『y<x+1』の直線グラフと、『y>2x²-2』の放物線の重なる領域は、下図の斜線部分になります。


ア、イ、ウの3式によって示される直線と放物線は、図の様に平面を①から⑧まで8つの領域に分かれる。これらの領域は、ア、イ、ウの3式の等号を適宣不等号に置き換えて得られる1組の連立不等式によって示される。ただし、領域とは図中の太い境界線は含まないものとする。[設問1]ア、イ、ウの式の等号をすべて不等号に置き換えて④の領域を表したときに、右開きの不等号(<)がつくのは次のうちどれか?[設問2]次の3式からなる連立不等式によって表される領域はどこか?

ア、イ、ウの3式によって示される関数がある。3式が示すグラフは右図の通りである。[設問1]ア、イ、ウの3つの等号を全て不等号に置き換えて⑥+⑧の領域になるようにしたい。このとき不等号が(<)の向きになるのはア、イ、ウのうちどの式か?[設問2]次の不等式に当てはまる領域はどこか?

①、②、③の3式によって示される関数がある。3式が示すグラフは右図の通りである。[設問1]A、B、Cの各点の座標はどれになるか?△ABCの面積はいくつになるか?

ア、イ、ウの3式によって示される直線と円は、図の様に平面を①から⑧まで8つの領域に分かれる。[設問1]ア、イ、ウの式の等号をすべて不等号に置き換えて⑦の領域(図のピンク色の部分)を表したときに、右開きの不等号(<)がつくのは次のうちどれか?[設問2]次の3式からなる連立不等式によってあらわされる領域はどこか?

SPI練習問題-問2(グラフの領域) 次の3つの式によって示される放物線と直線は、下図の様に平面を8つの領域に分ける。 ア y=x² イ y=x+2 ウ y=0 次の2式からなる連立不等式であらわされる領域はどれか? カ […]








