SPI練習問題-問5(グラフの領域)

SPI練習問題-問5(グラフの領域)

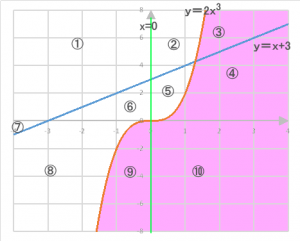
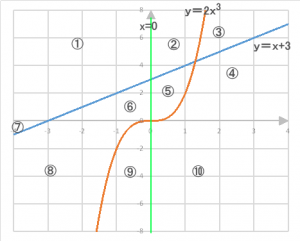ア、イ、ウの３式によって示される関数がある。３式が示すグラフは右図の通りである。

ア　ｙ＝ｘ＋３
イ　ｘ＝０
ウ　ｙ＝２ｘ³

[設問１]ア、イ、ウの３つの等号を全て不等号に置き換えて⑥＋⑧の領域になるようにしたい。このとき不等号が（＜）の向きになるのはア、イ、ウのうちどの式か？

[設問２]次の不等式に当てはまる領域はどこか？

ア　ｙ＜ｘ＋３
イ　ｘ＞０
ウ　ｙ＜２ｘ³

解答と解説

解答と解説

『グラフの領域』の問題の解き方や、使う公式に関しては『SPI グラフの領域 ～練習問題と解き方を徹底解説！～』のページで詳しく解説しています。解き方が分からない方は、まず、そちらのページを一読してください。

設問１の解答と解説：

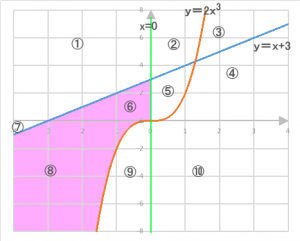⑥＋⑧の領域は、右図のピンク色の領域になります。このピンクの領域が各グラフの上に位置するのか、下に位置するのかを見ていきましょう。

ｙ＝ｘ＋３
ピンク色の領域は、グラフより下の領域（ｙ軸が下）にあるので、ｙ＜ｘ＋３となります。よって、不等号は、（＜）となり該当する。

ｘ＝０
ピンク色の領域は、ｘ＝０のグラフより左の領域（ｘが０より小さい領域）にあり、ｘ＜０となります。よって、不等号は、（＜）となり該当する。

ｙ＝２ｘ³
ピンク色の領域は、ｙ＝２ｘ³より上の領域（グラフよりｙ軸が上の領域）にあり、ｙ＞２ｘ³となります。よって、不等号は、（＞）となり該当しない。

求める解答は、ア、イのグラフのみが該当するのでＤが正解となる。

解答：Ｄ

設問２の解答と解説：

ア、イ、ウの各グラフに該当する領域を見ていきます。

ｙ＜ｘ＋３
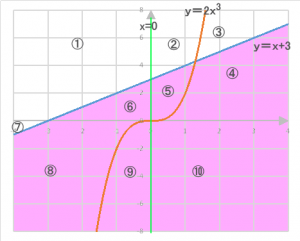グラフより下の領域（ｙ軸が下になる領域）を示しているので、右図のピンク色の領域が該当します。よって、④⑤⑥⑧⑨⑩。

ｘ＞０
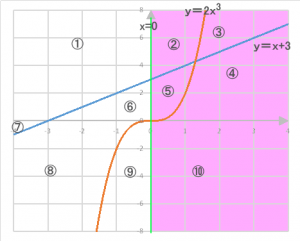ｘが０より大きい領域を指すので、右図のピンク色の領域が該当します。よって、②③④⑤⑩。

ｙ＜２ｘ³
グラフよりｙ軸が下の領域を指すので、右図のピンク色の領域が該当します。よって、③④⑨⑩。

もとめる解答は、これら３つのグラフに該当している領域のうち、全てに共通して当てはまる領域になります。よって、共通して当てはまる領域は④と⑩。該当する選択肢がないので、Ｈが正解。

解答：Ｈ