SPI練習問題-問3(グラフの領域)

SPI練習問題-問3(グラフの領域)

ア、イ、ウの３式によって示される直線と円は、図の様に平面を①から⑧まで８つの領域に分かれる。

ア　ｘ² ＋ y² ＝９²
イ　ｙ＝－ｘ－３
ウ　ｘ＝０

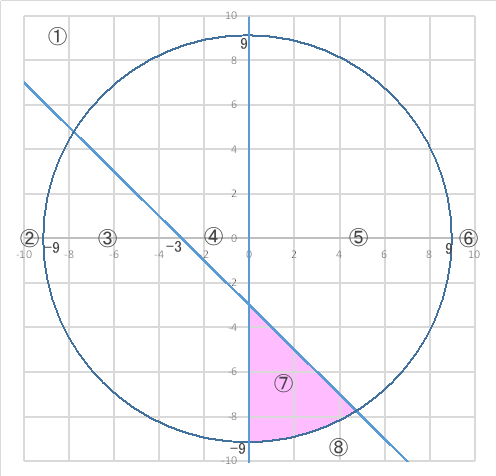
これらの領域は、ア、イ、ウノ３式の等号を適宣不等号に置き換えて得られる１組の連立不等式によって示される。

[設問１]ア、イ、ウの式の等号をすべて不等号に置き換えて⑦の領域（図のピンク色の部分）を表したときに、右開きの不等号（＜）がつくのは次のうちどれか？

[設問２]次の３式からなる連立不等式によってあらわされる領域はどこか？

カ　ｘ² ＋ y² ＞９²
キ　ｙ＞－ｘ－３
ク　ｘ＜０

解答と解説

ポイント：
直線グラフや円グラフの不等号によって、どの領域をさしているのかは理解しておきましょう。

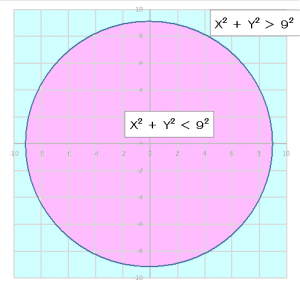
円グラフの場合は、右図の様にＸとＹの２乗の合計が右辺より小さければ縁の内側の領域を指します。逆の場合は外側になります。

Ｘ＞０のグラフは、Ｘは０より大きいことを意味するのでＸ＝０のグラフより右側の領域を指します。これは簡単ですね。

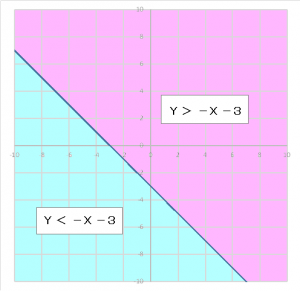
Ｙ＞－ｘ－３も考え方は同じで－ｘ－３よりもＹの方が大きいということは、Ｙ＝－ｘ－３の線よりもＹ軸が上の部分を示すので上側の領域になります。逆は、下側の領域。

設問１の解答と解説：

円グラフｘ² ＋ y² ＝９²に関してですが、領域⑦は、円グラフの内側にあるので不等号としては、（＜）が付きます。

直線グラフｙ＝－ｘ－３に関してですが、線グラフより下の領域なので、－ｘ－３よりｙの方が小さくなるので（＜）が付きます。

直線グラフｘ＝０に関してですが、直線グラフより右側の領域を指すので、ｘは０より大きいことになりますよって、ｘ＞０となるので（＞）がつきます。

よって、解答としては、アとイが（＜）となるのでＤが正解。分からない場合は、上記に記載したポイントを再度確認して下さい。

解答：Ｄ

設問２の解答と解説：

カ　円グラフｘ² ＋ y² ＞９² は円の外側をさします。よって、①②⑥⑧。

キ　直線グラフｙ＞－ｘ－３は、ｙの方が大きいということなので、直線グラフよりｙ軸が上の領域になります。よって、①④⑤⑥

ク　直線グラフｘ＜０は、ｘが０より小さい領域なので直線グラフより左側の領域を指します。よって、①②③④

カ、キ、ク全ての領域を満たすのは①のみになります。

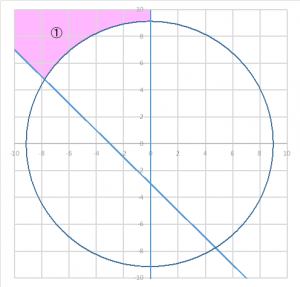
よって、Ａが正解。分からない場合は、上記に記載したポイントを再度確認して下さい。

解答：Ａ