SPI練習問題-問4(グラフの領域)
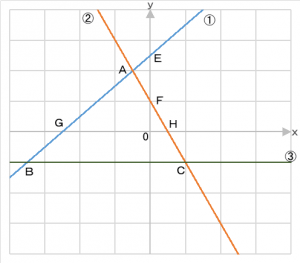 ①、②、③の3式によって示される関数がある。3式が示すグラフは右図の通りである。
①、②、③の3式によって示される関数がある。3式が示すグラフは右図の通りである。
① y=x+5
② y=-2x+2
③ y=-2
[設問1]A、B、Cの各点の座標はどれになるか?
A A(-2, 4)、B(-6, -3)、C(2, -2)
B A(-2, 5)、B(-6, -4)、C(2, -3)
C A(-1, 4)、B(-7, -2)、C(2, -2)
D A(-1, 5)、B(-7, -3)、C(2, -3)
E A(-3, 4)、B(-6, -3)、C(2, -2)
F A(-3, 5)、B(-6, -2)、C(1, -2)
G A(-1, 4)、B(-7, -3)、C(2, -2)
H いずれでもない
[設問2]△ABCの面積はいくつになるか?
A 25
B 26
C 27
D 28
E 29
F 30
G 31
H いずれでもない
解答と解説
ポイント:
★各グラフの交点の座標は連立方程式でもとめます。
★面積は、x軸、y軸の交点の座標を「長さ」や「高さ」に使う。
『グラフの領域』の問題の解き方や、使う公式に関しては『SPI グラフの領域 ~練習問題と解き方を徹底解説!~』のページで詳しく解説しています。解き方が分からない方は、まず、そちらのページを一読してください。
設問1の解答と解説:
Aの交点
Aの交点は、①と②のグラフの交点なので、この2つのグラフの方程式より、座標をもとめます。
① y=x+5
② y=-2x+2
x、yのどちらから求めても構いません。ただ、この場合であればxを先に求める方が楽そうですね。①式のyに②の式を代入します。
-2x+2=x+5
-3x=3
x=-1
xが求まったので、①の式にxの値を代入し、yの値を求めます。
y=-1+5=4
よって、Aの交点は、(-1, 4)
Bの交点
Bの交点は、①と③のグラフの交点なので、この2つのグラフの方程式より、座標をもとめます。
① y=x+5
③ y=-2
同様に①式のyに②の式を代入し、xを求めます。
-2=x+5
x=-7
①式にxの値を代入し、yを求めます。(③のグラフは、常に-2しかとらないので計算しなくても-2になることは分かる)
y=-7+5=-2
よって、Bの交点は、(-7, -2)
Cの交点
Cの交点は、②と③のグラフの交点なので、この2つのグラフの方程式より、座標をもとめます。
② y=-2x+2
③ y=-2
②の式のyに③式を代入します。
-2=-2x+2
2x=4
x=2
②式にxの値を代入し、yを求めます。
y=-2x2+2=-2
よって、Cの交点は、(2, -2)
求める解答は、A(-1, 4)、B(-7, -2)、C(2, -2)でCとなります。
解答:C
設問2の解答と解説:
△ABCの面積を求める為には、底辺と高さが必要になります。底辺をBC、高さをAZとし、まずはそれぞれの長さを求めます。
BCの長さC点のX座標が2、B点のX座標が-7。よって、BC間の長さは2+7=9となります。間違っても2-7=5としないように。B点のx座標-7というのはあくまで座標の位置であり、長さは絶対値の7になります。
また、高さは、A点からまっすぐ下に線を引きBグラフに垂直に交わる点をZ点とした、AZになります。よって、A点から垂直に線を引いているのでx座標はA点と同じ-2。y軸はBグラフとの交点なので-2だという事がすぐわかります。
A点のy座標4、Z点のy座標-2より、高さは4+2の6となります。底辺の時と同様に4-2=2としないように。
よって、求める△ABCの面積は、
底辺9x高さ6÷2=27
解答:C




