SPI練習問題-問11(推論・論証)
推論(平均)に関する問題。次の設問1を解答せよ。
購入した3種類の洋服P、Q、Rの値段について次のことが分かっている。
ⅰ)PとQの値段の平均は4,700円である。
ⅱ)P、Q、Rの値段の平均は5,800円である。
[設問1]3種類の洋服について必ず正しいと言えることは、次のア、イ、ウのうちどれか?A~Hの中から1つ選びなさい。
ア:PとRの値段の差は900円より大きい。
イ:3つの中で最も値段が高いのはRである。
ウ:3つの中で最も値段が安いのはRである。
A アだけ
B イだけ
C ウだけ
D アとイの両方
E アとウの両方
F イとウの両方
G アとイとウのすべて
H 該当なし
解答と解説
『推論・論証』の問題の解き方や、使う公式に関しては『SPI 推論・論証 ~練習問題と解き方を徹底解説!~』のページで詳しく解説しています。解き方が分からない方は、まず、そちらのページを一読してください。
設問1の解答と解説:
推論の問題を解く上で大切なことは、頭の中で考えるのではなく、まず確実に分かっていることを図式化または、数式化することです。今回の問題であれば、設問内容より、以下のことが分かっています。
ⅰ)PとQの値段の平均は4,700円である。
ⅱ)P、Q、Rの値段の平均は5,800円である。
この2点を数式化していきます。
まず、『PとQの値段の平均は4,700円である。』という点より、以下の式が成り立ちます。
(P+Q)÷2=4700
P+Q=4700×2
P+Q=9400 ・・・①
真面目に計算しましたが、2つのアイテムの平均が4,700円であれば、合計金額は9,400円と頭の中でも計算できますよね。
同様に『P、Q、Rの値段の平均は5,800円である。』という点より、以下の式が成り立ちます。
(P+Q+R)÷3=5800
P+Q+R=5800×3
P+Q+R=17400・・・②
式①で『P+Q=9400』と分かっているので、これを式②に代入してRの値段を求めます。
P+Q+R=17400・・・②
9400+R=17400
R=17400-9400
R=8000・・・③
式①②③を踏まえてア~ウを順に確認していきます。
P+Q=9400 ・・・①
P+Q+R=17400・・・②
R=8000・・・③
ア:PとRの値段の差は900円より大きい。
Rは8000円なので、「PとRの値段の差は900円より大きい」ということは、Pの値段は、以下のどちらかになります。
P>8900
P<7100
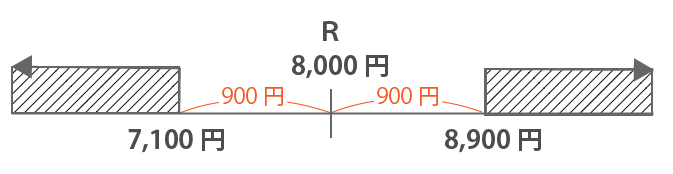
このことより、もし、Pの値段が以下の範囲内だとアの条件は否定され、必ずしも正しいとは言えないことになります。
7100<P<8900
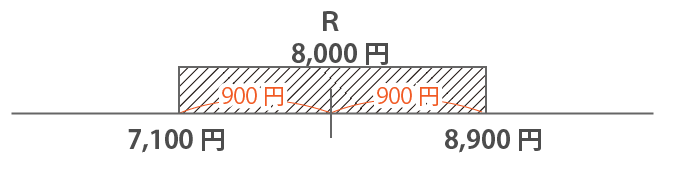
では、Pを「7100<P<8900」の範囲内である8000と仮定した場合、式①より、Qは1400となります。さらに式②も③も満たすのでP=8000は成り立ちます。
よって、「PとRの値段の差は900円より大きい」は必ずしも正しいと言えない。
イ:3つの中で最も値段が高いのはRである。
「R=8000」なので、PもしくはQのどちらかが8000以上であれば、イの条件は否定され必ずしも正しいとは言えないことになります。
では、例としてP=9000として仮定します。
「P+Q=9400」なので、P=9000のとき、Q=400となり、式①②③を全て満たすことができます。よって、P=9000、Q=400というのはあり得る組み合わせなので、イの条件は必ずしも正しいと言えない。
ウ:3つの中で最も値段が安いのはRである。
先程、P=9000、Q=400というのはあり得る組み合わということでしたよね。よって、Rより安いパターンは存在するので、ウの条件は否定され必ずしも正しいと言えない。
よって、ア、イ、ウのどの条件も必ずしも正しいとは言えないので、解答はHとなる。
解答:H




