SPI練習問題-問10(推論・論証)
推論(内訳)に関する問題。次の設問1と設問2を解答せよ。
リンゴとキウイ、モモの3種類の果物を合わせて9個買った。3種類の果物について、次のことが分かっている。
ⅰ)3種類とも少なくとも1個は買った。
ⅱ)キウイはリンゴの個数より少ない。
[設問1]次の推論ア、イ、ウのうち、必ず正しいと言えるものはどれか?A~Hの中から1つ選びなさい。
ア:モモが2個ならば、キウイは3個である。
イ:モモが4個ならば、キウイは2個である。
ウ:モモが5個ならば、キウイは1個である。
A アだけ
B イだけ
C ウだけ
D アとイの両方
E アとウの両方
F イとウの両方
G アとイとウのすべて
H 該当なし
[設問2]次の推論ア、イ、ウのうち、必ず正しいと言えるものはどれか?A~Hの中から1つ選びなさい。
ア:キウイとモモの数が同じならば、リンゴは5個である。
イ:リンゴとモモの数が同じならば、キウイは1個である。
ウ:モモの数がリンゴより2個以上多いならば、キウイは1個である。
A アだけ
B イだけ
C ウだけ
D アとイの両方
E アとウの両方
F イとウの両方
G アとイとウのすべて
H 該当なし
解答と解説
『推論・論証』の問題の解き方や、使う公式に関しては『SPI 推論・論証 ~練習問題と解き方を徹底解説!~』のページで詳しく解説しています。解き方が分からない方は、まず、そちらのページを一読してください。
設問1の解答と解説:
推論の問題を解く上で大切なことは、頭の中で考えるのではなく、まず確実に分かっていることを図式化することです。今回の問題であれば、設問内容より、以下のことが分かっています。
ⅰ)3種類とも少なくとも1個は買った。
ⅱ)キウイはリンゴの個数より少ない。
この2点を図式化していきます。
まず、『3種類とも少なくとも1個は買った。』という点より、以下が確定します。
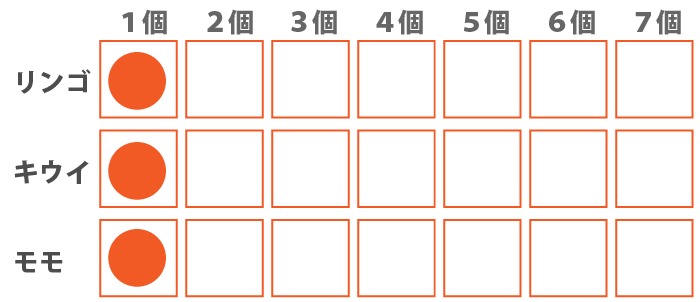
更に『キウイはリンゴの個数より少ない。』という点からリンゴは、少なくとも2個以上が確定します。
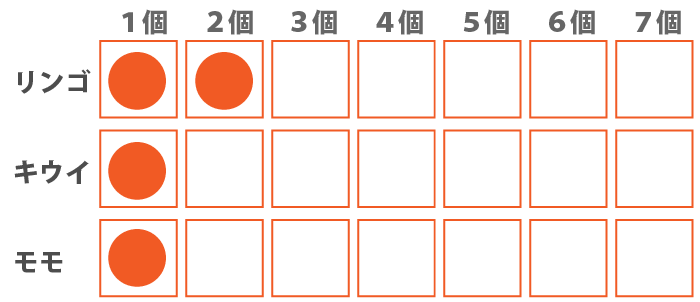
この情報を踏まえて、ア~ウを確認していきます。
ア:モモが2個ならば、キウイは3個である。
モモが2個の場合、キウイは3個しかあり得なければ、『必ず正しいと言える』のですが、他のパターンがあれば必ず正しいとは言えないことになります。全パターンを洗い出す必要はなく、1つでもあり得ないパターンを見つければ、その時点でアは違うと判断して次に進みましょう。
モモが2個の場合、リンゴが6個、キウイが1個というパターンが少なくともあり得るので、アは必ずしも正しいとは言えない。
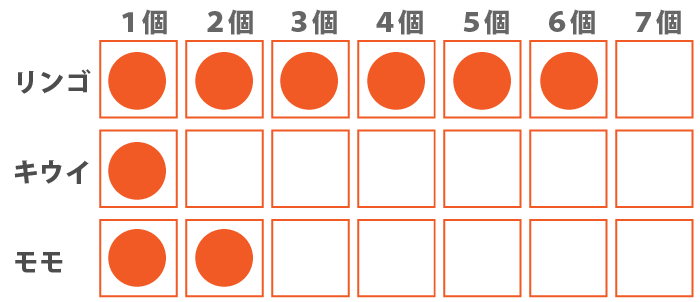
イ:モモが4個ならば、キウイは2個である。
モモが4個の場合、キウイは2個しかあり得なければ、『必ず正しいと言える』のですが、他のパターンがあれば必ず正しいとは言えないことになります。全パターンを洗い出す必要はなく、1つでもあり得ないパターンを見つければ、その時点でアは違うと判断して次に進みましょう。
モモが4個の場合、リンゴが4個、キウイが1個というパターンが少なくともあり得るので、イは必ずしも正しいとは言えない。
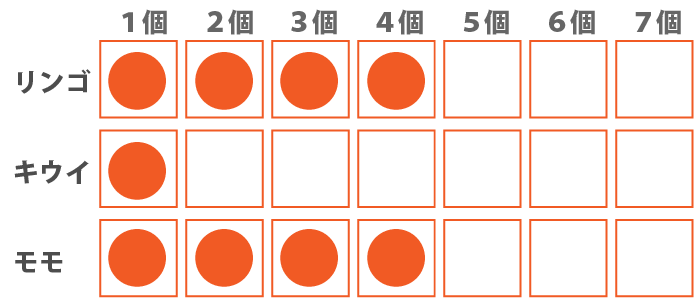
ウ:モモが5個ならば、キウイは1個である。
モモが5個の場合、キウイは1個しかあり得なければ、『必ず正しいと言える』のですが、他のパターンがあれば必ず正しいとは言えないことになります。
モモが5個の場合、残り4個がリンゴとキウイになります。もし、それぞれが2個ずつだと、『キウイはリンゴの個数より少ない。』の条件に反してしまうため、リンゴが3個、キウイが1個しかあり得ないことになります。
よって、モモが5個ならば、キウイは1個というのは必ず正しいと言えます。
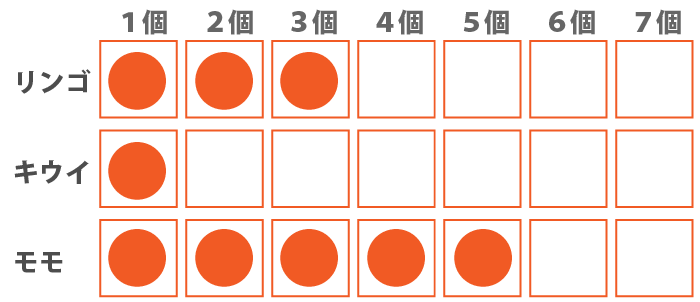
よって、求める解答はウだけのCとなります。
解答:C
設問2の解答と解説:
設問1と同様で、以下のことが分かっています。
ⅰ)3種類とも少なくとも1個は買った。
ⅱ)キウイはリンゴの個数より少ない。
よって、最初の段階でリンゴが2個以上、キウイとモモが各1個以上というのは確定しています。問題は、残り5個がどこに割り振られるかになります。

ア~ウを順に確認していきます。
ア:キウイとモモの数が同じならば、リンゴは5個である。
キウイとモモが各2個ずつであればリンゴは5個となりますが、キウイとモモが各1個ずつの場合、リンゴは7個となるため、必ずしも正しいとは言えない。
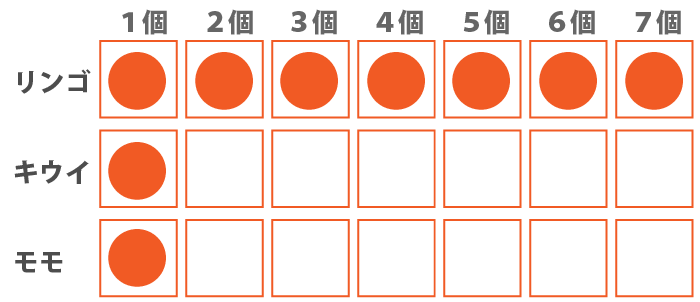
イ:リンゴとモモの数が同じならば、キウイは1個である。
リンゴとモモが各4個ずつの場合、キウイは1個となる。リンゴとモモが各3個ずつの場合は、キウイも3個となるため『キウイはリンゴの個数より少ない。』の条件を満たさない。さらにリンゴとモモが各5個以上になると、9個を超えてしまうためあり得ない。
よって、『リンゴとモモの数が同じならば、キウイは1個』というのは、必ず正しいと言えると言える。
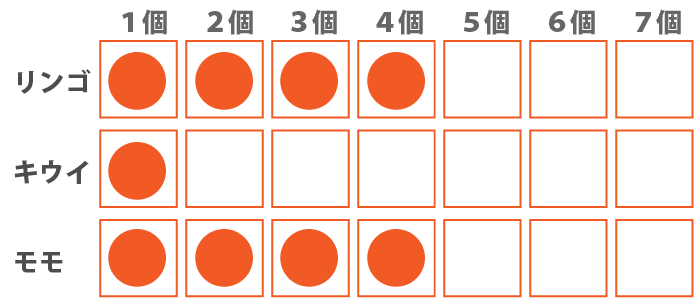
ウ:モモの数がリンゴより2個以上多いならば、キウイは1個である。
要は、モモの数がリンゴより2個以上多い時にキウイの数が2個以上のパターンがあれば、この条件は当てはまらないということになります。
モモの数がリンゴより2個以上多い場合、少なくともリンゴが2個以上、キウイが1個以上、モモが4個以上というのは確定します。
では、キウイが2個の時、モモの数がリンゴより2個以上多い組み合わせが無いか確認します。
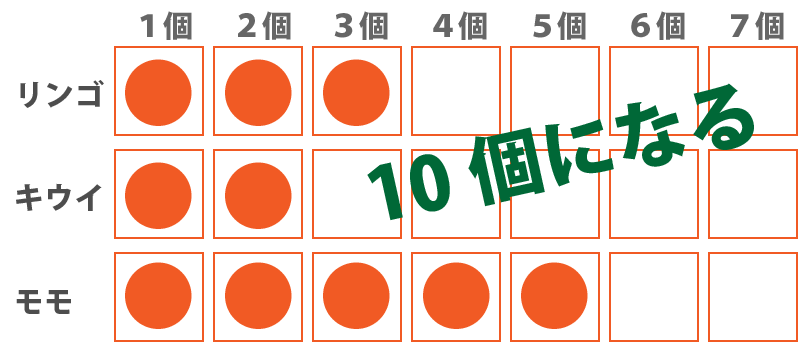
キウイが2個になるとき、リンゴはキウイより数が多くなければならないので、リンゴは3個以上になります。更にリンゴが3個以上の場合、モモも5個以上でないと駄目ということになります。そうすると果物の数が10個以上となるためキウイが2個というのはあり得ないということになります。
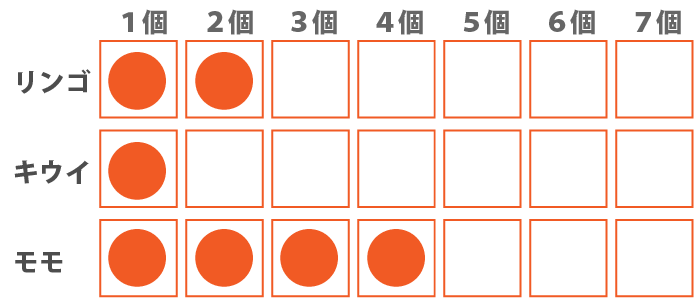
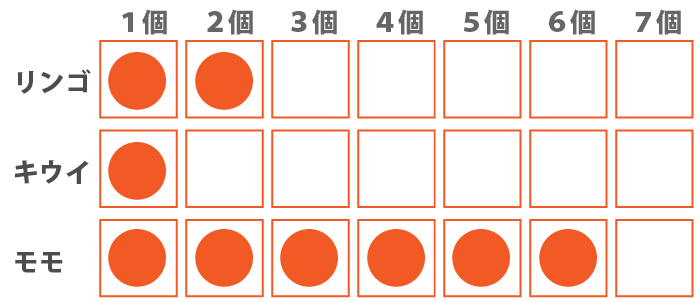
では、残り2個を両方ともモモに割り振った場合、リンゴが6個、キウイが1個、モモが2個となり、条件を満たしています。
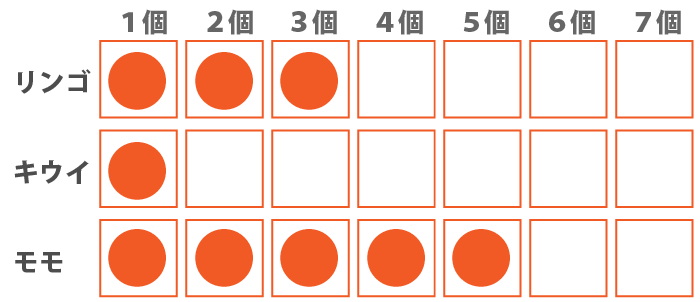
また、残り2個をリンゴとモモに各1こずつ割り振った場合もリンゴ3個、キウイが1個、モモが5個と条件を満たします。
よって、『モモの数がリンゴより2個以上多い場合、キウイは必ず1個である』という条件は必ず正しいと言えます。
よって、求める解答はイとウのFとなります。
解答:F




