SPI練習問題-問4(集合)

SPI練習問題-問4(集合)

集合の問題。次の問いを解答せよ。

ある地区の150軒の家でＰ、Ｑ、Ｒの新聞を取っているかどうかの調査を行った。Ｐ新聞を取っている家が62軒、Ｑ新聞を取っている家が78軒、Ｒ新聞を取っている家が54 軒、三紙すべて取っている家が16軒あった。その一方で、三紙とも取っていない家が10軒あった

[問題１]
Ｐ、Ｑ、Ｒのいずれか二紙のみ取っている、家は何軒あるか。

解答と解説

『集合』の問題の解き方や、使う公式に関しては『SPI 集合 ～練習問題と解き方を徹底解説！～』のページで詳しく解説しています。解き方が分からない方は、まず、そちらのページを一読してください。

設問の解答と解説：

分かっている内容をベン図にすると次のようになります。

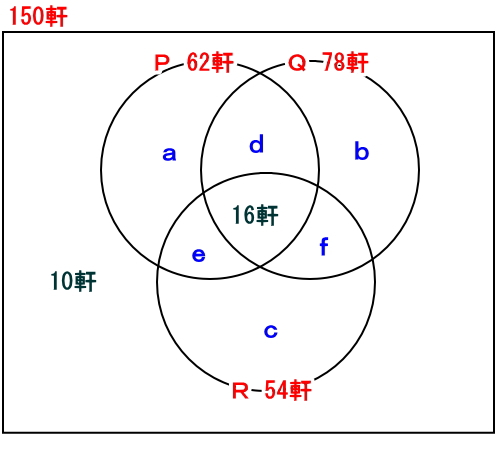
　ａは、Ｐ新聞だけを取っている家
　ｂは、Ｑ新聞だけを取っている家
　ｃは、Ｒ新聞だけを取っている家
　ｄは、ＰとＱ新聞を取っている家
　ｅは、ＰとＲ新聞を取っている家
　ｆは、ＱとＲ新聞を取っている家

求めたいのは、Ｐ、Ｑ、Ｒのいずれか二紙のみ取っている、家の軒数なので該当するのは、ｄ、ｅ、ｆになります。

まずは、Ｐ新聞、Ｑ新聞、Ｒ新聞を個別にみていきます。

Ｐ新聞
Ｐ新聞を取っている家の合計軒数は、62軒。その内訳は、

　Ｐ新聞のみを取っているａ
　Ｐ新聞とＱ新聞を取っているｄ
　Ｐ新聞とＲ新聞を取っているｅ
　Ｐ新聞とＱ新聞とＲ新聞を取っている16軒

この合計が62軒となるので次の式が成り立ちます。

　ａ＋ｄ＋ｅ＋16＝62
　　↓
　ａ＋ｄ＋ｅ＝62－16
　ａ＋ｄ＋ｅ＝46 ・・・(１)

Ｑ新聞
Ｑ新聞を取っている家の合計軒数は、78軒。その内訳は、

　Ｑ新聞のみを取っているｂ
　Ｑ新聞とＰ新聞を取っているｄ
　Ｑ新聞とＲ新聞を取っているｆ
　Ｐ新聞とＱ新聞とＲ新聞を取っている16軒

この合計が78軒となるので次の式が成り立ちます。

　ｂ＋ｄ＋ｆ＋16＝78
　　↓
　ｂ＋ｄ＋ｆ＝78－16
　ｂ＋ｄ＋ｆ＝62 ・・・(２)

Ｒ新聞
Ｒ新聞を取っている家の合計軒数は、54軒。その内訳は、

　Ｒ新聞のみを取っているｃ
　Ｒ新聞とＰ新聞を取っているｅ
　Ｒ新聞とＱ新聞を取っているｆ
　Ｐ新聞とＱ新聞とＲ新聞を取っている16軒

この合計が54軒となるので次の式が成り立ちます。

　ｃ＋ｅ＋ｆ＋16＝54
　　↓
　ｃ＋ｅ＋ｆ＝54－16
　ｃ＋ｅ＋ｆ＝38 ・・・(３)

さらに円内の合計軒数は上図のａ、ｂ、ｃ、ｄ、ｅ、ｆ、16軒の合計になります。この合計軒数は、聞き取りをした家の軒数は150軒でその内10軒が円の外になるので、150－10＝140軒となります。よって、円内の合計軒数は次の式で表すことができます。

　ａ＋ｂ＋ｃ＋ｄ＋ｅ＋ｆ＋16＝140
　　↓
　ａ＋ｂ＋ｃ＋ｄ＋ｅ＋ｆ＝140－16
　ａ＋ｂ＋ｃ＋ｄ＋ｅ＋ｆ＝124 ・・・(４)

求めたいのは、Ｐ、Ｑ、Ｒのいずれか二紙のみ取っている、家の軒数ｄ、ｅ、ｆの合計軒数です。よって、式(４)をｄ、ｅ、ｆの合計となるように変形させます。

　ａ＋ｂ＋ｃ＋ｄ＋ｅ＋ｆ＝124 ・・・(４)
　ｄ＋ｅ＋ｆ＝124－(ａ＋ｂ＋ｃ) ・・・(５)
　

ｄ＋ｅ＋ｆの合計を求めるには、ａ＋ｂ＋ｃの値が分かる必要があります。そこで、上で求めた式(１)(２)(３)を利用します。

　ａ＋ｄ＋ｅ＝46 ・・・(１)
　ｂ＋ｄ＋ｆ＝62 ・・・(２)
　ｃ＋ｅ＋ｆ＝38 ・・・(３)

この式(１)(２)(３)を変形させると

　ａ＝46－ｄ－ｅ ・・・(１)’
　ｂ＝62－ｄ－ｆ ・・・(２)’
　ｃ＝38－ｅ－ｆ ・・・(３)’

となります。これを式(５)へ代入します。

　ｄ＋ｅ＋ｆ＝124－{(46－ｄ－ｅ)＋(62－ｄ－ｆ)＋(38－ｅ－ｆ)}

　ｄ＋ｅ＋ｆ＝124－(46－ｄ－ｅ＋62－ｄ－ｆ＋38－ｅ－ｆ)
　ｄ＋ｅ＋ｆ＝124－(146－2ｄ－2ｅ－2ｆ)
　ｄ＋ｅ＋ｆ＝124－146＋2ｄ＋2ｅ＋2ｆ)
　ｄ＋ｅ＋ｆ－2ｄ－2ｅ－2ｆ＝－22
　－ｄ－ｅ－ｆ＝－22
　－(ｄ＋ｅ＋ｆ)＝－22
　ｄ＋ｅ＋ｆ＝22

よって、22軒

解答：Ｃ