SPI練習問題-問7(速度算)
家から図書館を通ってデパートまでの道のりは4kmあり、兄は家から図書館までを平均80m/分、図書館からデパートまでを平均60m/分で歩いたところ、1時間かかった。私は同じ道をデパートから図書館を通り家に行くのに75m/分で歩いた。
[設問1]
私と兄が同時に出発すると、出会うのは何分後か?
解答と解説
速度算の問題の解き方や、使う公式に関しては『SPI 速度算 ~練習問題と解き方を徹底解説!~』のページで詳しく解説しています。解き方が分からない方は、まず、そちらのページを一読してください。
設問1の解答と解説:
まずは、距離が『km』や『m』、時間が『時間』や『分』と統一されていないので、注意。違う単位どうしを掛けたり、足したりするとその時点で誤った解答になってしまいます。今回は求める解答が『分』なので、時間の単位は『分』で統一。距離は、『m』で統一して計算します。
求めたいのは、両者反対の方向から同時にスタートした場合、両社が遭遇するのはスタートから何分後か?図にすると下図の通りです。

まず、『家から図書館までの距離』と『図書館からデパートまでの距離』を求めます。家から図書館までの距離をLとした場合、図書館からデパートまでの距離は4000-Lとなります。図にすると下図の通り。
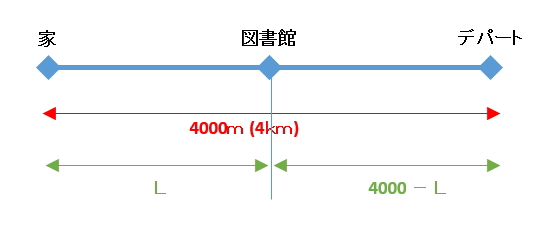
そして、兄はこの家からデパートまで移動するのに1時間かかったということなので次の式が成り立ちます。(分で統一するので1時間は60分に変換)
60分 = (家から図書館までの時間) + (図書館からデパートまでの時間) …(1)
公式③より、
家から図書館までの時間 = L ÷ 80
図書館からデパートまでの時間 = (4000-L) ÷ 60
これを式(1)に代入すると、
60 = (L ÷ 80) + {(4000-L) ÷ 60}
この式を解くと距離Lが算出できます。
60 = (L ÷ 80) + {(4000-L) ÷ 60}
60 = L/80 + 4000/60 - L/60
計算しやすいように両辺に240を掛けて分母を無くします。
14400 = 3L + 16000 - 4L
L = 1600m
よって、家から図書館までの距離は1600m。更に図書館からデパートまでの距離は、
4000m - 1600m = 2400m
というのが分かります。
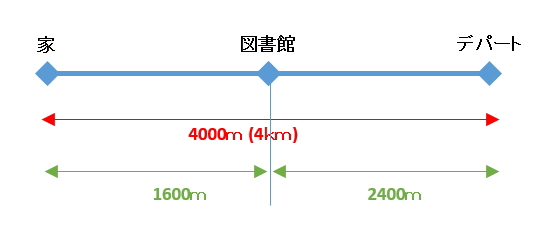
兄は、家から図書館まで時速80m/分で移動しているので、家から図書館に着くまでにかかる時間は、公式③より、20分と分かります。
家から図書館に着くまでにかかる時間 = 1600 ÷ 80 = 20分
この時点で私が移動している距離は、公式①より、1500mだと分かります。
私が20分で移動した距離 = 75 × 20 = 1500m
図にすると下図の通りで、20分経過した時点ではまだ遭遇しておらず残り900mの距離があることが分かります。
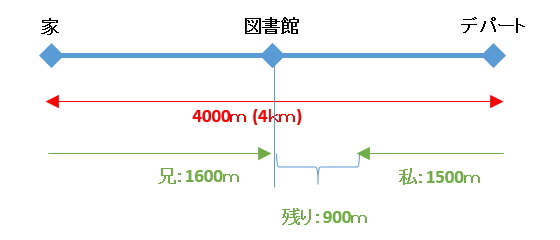
この残り900mの区間のどこかで遭遇することになるのですが、両社とも移動するのでこの900mは次の式で表すことができます。
900m = 兄の移動距離 + 私の移動距離
この式は、公式①より、次のようになります。移動にかかった時間をMとします。
900 = (60 × M) + (75 × M)
この式を解くと、移動にかかった時間Mが求まります。
900 = (60 × M) + (75 × M)
900 = 135M
M = 900/135 = 20/3 = 6分と2/3 = 6分40秒
もしくは、
M = 900/135 = 20/3 = 6.666666~ ≒6.7分
この時間は最後の900mで双方が遭遇するまでの時間であり、それまでに移動した20分があるので、20分を足す必要があります。よって、求める解答は、
26分40秒(もしくは、26.7分)
解答:26分40秒(もしくは、26.7分)




