SPI練習問題-問3(速度算・通過算)

SPI練習問題-問3(速度算)

電車がＡ駅を出て目的地Ｂ駅に向かって走る。Ａ駅をで出て１時間２０分たったＣ地点で信号機からの警告に気づき、速度を８分の５に落とした。そのためＢ駅には予定よりも１時間２７分遅れでついた。もしこの警告がＣ地点から２１６km Ｂ駅に近いD地点で起こっていたら遅れは一時間で済んだ。

[設問１]列車が速度を落とす前の速さはいくらか？

[設問２]ＡからＢ駅までの距離はいくらか？

解答と解説

速度算の問題の解き方や、使う公式に関しては『SPI 速度算 ～練習問題と解き方を徹底解説！～』のページで詳しく解説しています。解き方が分からない方は、まず、そちらのページを一読してください。

設問１の解答と解説：

速度を求めるためには、距離と時間が必須になります。問題を解くため考え方としては、この距離と時間が分かっている区間を利用するということです。距離が分かっているのは、Ｃ－Ｄ区間が２１６ｋｍのみなので、基本的にはこの区間を利用して問題を解くことを考えましょう。

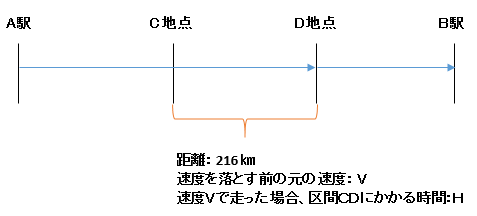
速度を落とす前の元の速度をＶ、その速度Ｖで区間Ｃ－Ｄを走行したさいにかかった時間をＨとした場合、時間Ｈは、次の２つの式で表すことができます。

　時間 ＝ 距離 ÷ 速度

　Ｈ ＝ ２１６ ÷ Ｖ ・・・（１）
（Ｈ ＋ ２７/６０）＝ ２１６ ÷（Ｖ ｘ ５/８） ・・・（２）

（１）式は、速度を落とす前の速度で区間ＣＤを走った場合の式です。（２）は、速度を落とし、区間ＣＤを走った場合の式です。

（１）式を（２）式に代入すると次のようになります。

（２１６ ÷ Ｖ ＋ ２７/６０）＝ ２１６ ÷（Ｖ ｘ ５/８）

更にこの式を解いていくと次のようになります。途中の細かい計算式も記載していますが、このあたりは自分が解きやすいように解けばよい。

　２１６/Ｖ ＋ ２７/６０ ＝ ２１６ ÷ ５Ｖ/８
　２１６/Ｖ ＋ ２７/６０ ＝ ２１６ ｘ ８/５Ｖ
　２１６/Ｖ ＋ ２７/６０ ＝ １７２８/５Ｖ
　２１６ ＋ ２７Ｖ/６０ ＝ １７２８/５
　２７Ｖ/６０ ＝ １７２８/５ － ２１６
　９Ｖ/２０ ＝ １７２８/５ － ２１６
　９Ｖ ＝ ６９１２ － ４３２０
　９Ｖ ＝ ２５９２
　Ｖ ＝ ２８８ｋｍ/ｈ

解答：Ｅ

設問２の解答と解説：

元の速度が２８８ｋｍ/ｈ
落とした速度が２８８ｋｍ/ｈ ｘ ５/８ ＝ １８０ｋｍ/ｈ

区間ＡＣの距離を求める
区間ＡＣは、落とす前の速度２８８ｋｍで走行し、１時間２０分かかるので次の式で表すことができます。（１時間２０分は、８０分。単位は分ではなく時間で表す必要があるので６０で割って８０/６０に書き換えることができる。）

区間ＡＣの距離 ＝ ２８８ ｘ（８０/６０）＝ ３８４ｋｍ ・・・（３）

区間ＣＢの距離を求める
区間ＣＢを速度を落とす前の速度２８８ｋｍで走った場合にかかる時間をＨ、距離をＬとすると次の式で表されます。

Ｌ ＝ ２８８ ｘ Ｈ　・・・（４）

区間ＣＢを速度を落とし１８０ｋｍで走った場合は次の式で表されます。

Ｌ ＝ １８０ ｘ（Ｈ ＋ ８７/６０）　・・・（５）

（４）（５）の式より、区間ＣＢの距離Ｌを求めます。（４）式より、Ｈ ＝ Ｌ ÷ ２８８ これを（５）式に代入します。

Ｌ ＝ １８０ ｘ（Ｌ ÷ ２８８ ＋ ８７/６０）
Ｌ ＝ １８０Ｌ/２８８ ＋ ２６１
Ｌ － １８０Ｌ/２８８ ＝ ２６１
１０８Ｌ/２８８ ＝ ２６１
Ｌ ＝ ２６１ ｘ ２８８/１０８ ＝ ６９６ｋｍ　・・・（６）

よって、区間ＡＢは、（３）＋（６）になるので、

区間ＡＢの距離 ＝ ３８４ｋｍ ＋ ６９６ｋｍ ＝ １０８０ｋｍ

解答：Ｅ