SPI練習問題-問11(n進法)

SPI練習問題-問11(n進法)

ｎ進法に関する問題。

[設問１] 5進法の14と10進法の25の和を7進法で表すといくつになるか？

[設問２] 2進法の111000と8進法の453の和を6進法で表すといくつになるか？

解答と解説

使用する公式：
ｎ進法の解き方に関しては、『SPI ｎ進法 ～練習問題と徹底解説！～』のページで詳しく解説しているので、参考にしてください。早く解く方法なども紹介しています。

設問１の解答と解説：

解き方の流れとしては、5進法の14をまずは10進法に変換し、10進法どうしの足し算をした後、7進法に変換するという流れになります。

STEP1. 5進法から10進法に変換する

(1×5¹)＋(4×5⁰)＝9

STEP2. 10進法どうしの足し算をする

9＋25＝34

STEP3. 10進法から7進法に変換する

よって、5進法の14と10進法の25の和を7進法で表すと46になる。

解答：Ｂ

設問２の解答と解説：

2進法の111000と8進法の453を一度、10進法に変換して足し算をした後に6進法に変換します。

STEP1. 10進法に変換する

2進法の111000を10進法に変換すると次の通り。

(1×2⁵)＋(1×2⁴)＋(1×2³)＋(0×2²)＋(0×2¹)＋(0×2⁰)
＝32＋16＋8＋0＋0＋0
＝56

上記は、次の変換方法を知っていると更に早く変換できます。詳しいやり方は、『ｎ進数から10進数への変換方法【別解-最速の解き方】』のページを参照してください。

掛け算と足し算の計算優先順位関係なしで前から順に計算していきます。
1×2＋1×2＋1×2＋0×2＋0×2＋0
＝2＋1×2＋1×2＋0×2＋0×2＋0
＝3×2＋1×2＋0×2＋0×2＋0
＝6＋1×2＋0×2＋0×2＋0
＝7×2＋0×2＋0×2＋0
＝14＋0×2＋0×2＋0
＝14×2＋0×2＋0
＝28＋0×2＋0
＝28×2＋0
＝56＋0
＝56

特殊な計算なので、一つずつ計算過程を描いたので一見、通常の解き方の方が早そうに見えてしまいますが、後者の方が圧倒的に簡単で早いです。

次に8進法の453を10進法に変換します。先程の後者の解き方で変換します。
4×8＋5×8＋3
＝32＋5×8＋3
＝37×8＋3
＝296＋3
＝299

STEP2. 10進法の足し算をする

2進法の111000と8進法の453を10進法に変換すると、56と299だったのでその和は次の通り。

56＋299＝355

STEP3. 6進法に変換する

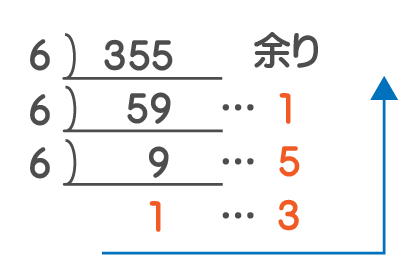
よって、2進法の111000と8進法の453の和を6進法で表すと1351になる。

解答：Ｆ