SPI練習問題-問2(グラフの領域)
次の3つの式によって示される放物線と直線は、下図の様に平面を8つの領域に分ける。
ア y=x²
イ y=x+2
ウ y=0
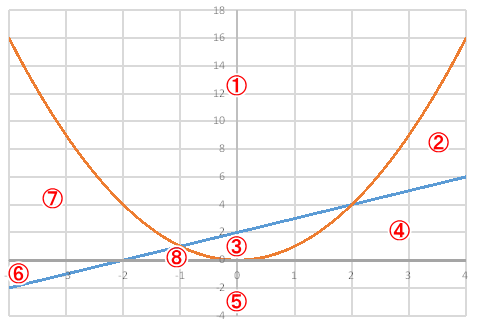
次の2式からなる連立不等式であらわされる領域はどれか?
カ y>x²
キ y<x+2
A ①のみ
B ②のみ
C ③のみ
D ④のみ
E ②と⑥と⑦
F ③と④と⑧
G ④と⑤と⑧
H いずれでもない
解答と解説
『グラフの領域』の問題の解き方や、使う公式に関しては『SPI グラフの領域 ~練習問題と解き方を徹底解説!~』のページで詳しく解説しています。解き方が分からない方は、まず、そちらのページを一読してください。
設問1の解答と解説:
連立方程式がどのグラフを指しているのか?また、不等号により、グラフのどこの領域を指しているのかは把握しておくようにしましょう。
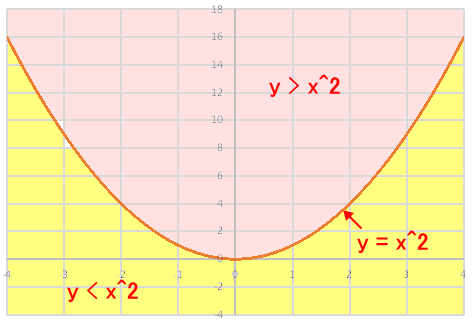
y= x² の方程式は下図の放物線のグラフを指しています。
また、これに不等号が加わり、y> x² となる場合は、ピンク色の領域を指します。x²の放物線よりもyの方が大きい(>)のでピンク色の領域ということですね。逆にy< x² となる場合は、黄色の領域を指します。x²の放物線よりもyの方が小さい(<)ので黄色の領域ということですね。
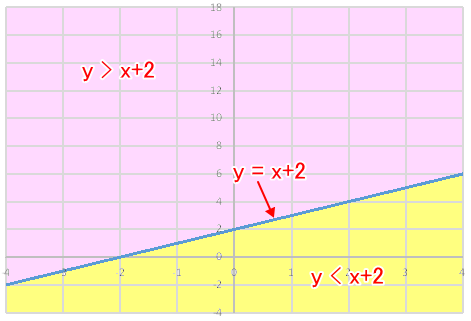
y=x+2 の方程式は下図の直線グラフを指しています。
放物線の時と考え方は同じで、y>x+2となる場合は、x+2よりもyの方が大きいということなので、グラフ線よりもy軸が上の領域を指します。逆にy<x+2となる場合は、x+2よりもyの方が小さいということなので、グラフ線よりもy軸が下の領域を指します。
そして、今回の設問では、下記の2式の領域ということなので、放物線のグラフよりY軸が上の領域かつ、直線グラフよりY軸が下の領域をさします。
カ y>x²
キ y<x+2
グラフにするとピンク色の領域ですね。
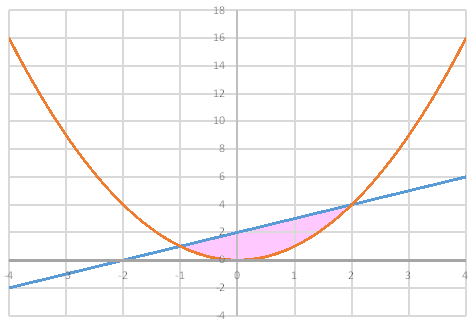
よって、解答としては③の領域のみなので、Cとなります。
解答:C




