SPI練習問題-問1(グラフの領域)

SPI練習問題-問1(グラフの領域)

ア、イ、ウの３式によって示される直線と放物線は、図の様に平面を①から⑧まで８つの領域に分かれる。

ア　ｙ＝－ｘ²＋４
イ　ｙ＝－２ｘ＋４
ウ　ｙ＝０

これらの領域は、ア、イ、ウの３式の等号を適宣不等号に置き換えて得られる１組の連立不等式によって示される。ただし、領域とは図中の太い境界線は含まないものとする。

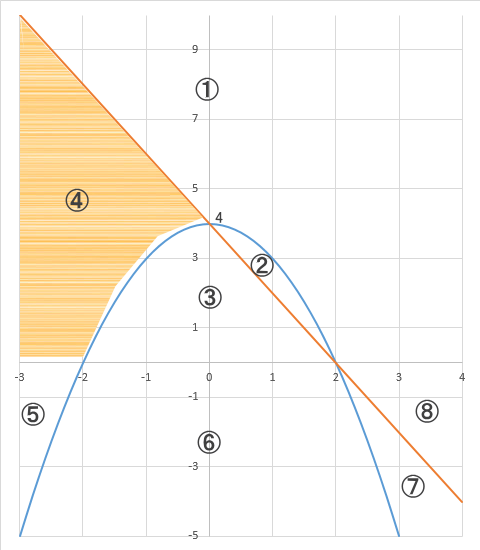
[設問１]ア、イ、ウの式の等号をすべて不等号に置き換えて④の領域を表したときに、右開きの不等号（＜）がつくのは次のうちどれか？

[設問２]次の３式からなる連立不等式によって表される領域はどこか？

カ　ｙ＜－ｘ²＋４
キ　ｙ＞－２ｘ＋４
ク　ｙ＞０

解答と解説

『グラフの領域』の問題の解き方や、使う公式に関しては『SPI グラフの領域 ～練習問題と解き方を徹底解説！～』のページで詳しく解説しています。解き方が分からない方は、まず、そちらのページを一読してください。

設問１の解答と解説：

ア　ｙ＝－ｘ²＋４
まず、ｙ＝－ｘ²＋４ですが、これは放物線のグラフでｙ＞－ｘ²＋４となります。分かりますでしょうか？実際に仮の値を入れて確認してもいいですが、一番確実で早い覚え方は、下向きの放物線の場合、放物線の外側はｙの方が大きくなります。

下向き放物線の場合、
　放物線の外側の領域：ｙ＞ａｘ²＋ｂ・・・（１）
　放物線の内側の領域：ｙ＜ａｘ²＋ｂ・・・（２）

上向き放物線の場合、
　放物線の外側の領域：ｙ＜ａｘ²＋ｂ・・・（３）
　放物線の内側の領域：ｙ＞ａｘ²＋ｂ・・・（４）

よって、今回は（１）が該当します。

イ　ｙ＝－２ｘ＋４
放物線と同様に直線グラフの場合も次の等号が成立します。

右上がりの直線グラフの場合
　直線グラフの上側の領域：ｙ＞ａｘ＋ｂ・・・（１）
　直線グラフの下側の領域：ｙ＜ａｘ＋ｂ・・・（２）

右下がりの直線グラフの場合
　直線グラフの上側の領域：ｙ＞ａｘ＋ｂ・・・（３）
　直線グラフの下側の領域：ｙ＜ａｘ＋ｂ・・・（４）

よって、今回は（４）が適用されます。

ウ　ｙ＝０
ｘ軸と並行の直線グラフの場合は、次の等号がなりたちます。簡単ですね。

　直線グラフの上側の領域：ｙ＞ｂ・・・（１）
　直線グラフの下側の領域：ｙ＜ｂ・・・（２）
　
よって、今回は（１）が適用されます。

これらの結果より、右開きになるのは、イだけになるため、求める解答はＢとなります。

解答：Ｂ

設問２の解答と解説：

それぞれ順番に領域を見ていきます。

カ　ｙ＜－ｘ²＋４
考え方は設問１と同じで下向きの放物線で右開きになっている場合、指し示す領域は放物線の内側になります。よって、②③⑥が該当します。

キ　ｙ＞－２ｘ＋４
右下がりのグラフで左開きの等号になるということは、直線グラフの上側にを示します。よって、①②⑧が該当します。

ク　ｙ＞０
Ｘ軸と並行なグラフで左開きの場合はグラフより上の領域をしめします。よって、①②③④が該当します。

これらより、３つの連立不等式全てに該当する部分は、②ということがわかります。よって、求める解答はＢとなります。

解答：Ｂ