何度も繰り返し解きましょう

条件と領域 練習問題集




条件と領域の練習問題を解く前にまずは、以下の内容をしっかりと熟読し、理解してから解くようにしてください。そうすることで、試験本番でもスムーズに解けるようになると思います。

SPI 条件と領域の問題の解き方

重要なポイント

  • 座標から直線の式が求められること

SPIの『条件と領域』の問題を解くには上記の1点が非常に重要になってきます。

何のことか分からないという人は、以下に詳しく解説しておくので熟読し理解するようにしてください。

座標から直線の式が求められること

直線の式

  • ｙ＝ａｘ+ｂ
    ａ：傾き
    ｂ：切片
  • ※傾きはグラフの傾き。ｙ座標の増加量ｘ座標の増加量で表される
  • ※切片はグラフとｙ軸との交点のｙ座標値

上の式は直線の式の基本形です。必ず覚えておくようにしてください。

では、下図の様なＡ点とＢ点の2点を通る直線の式を求められますか？

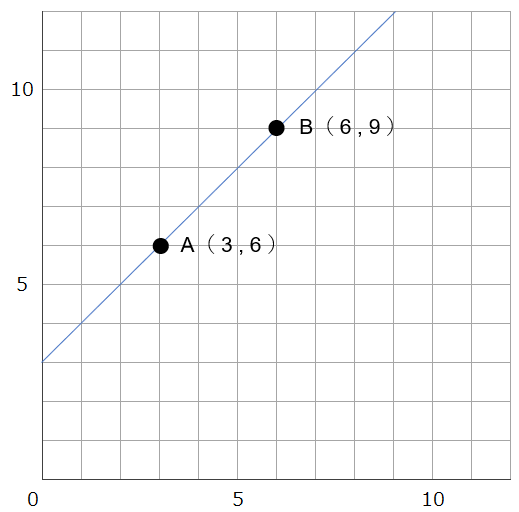
SPI 条件と領域 2点を通る直線の式

切片はグラフとｙ軸との交点のｙ座標値なので、3だとすぐにわかると思います。

次にグラフの傾きですが、点Ａから点Ｂへは、ｘ側に3、ｙ側に3移動しているので、傾きは33＝1 となります。

よって、直線の式は、
ｙ＝ｘ+3

できれば覚えておいて欲しい公式

二点を通る直線の式

  • 座標平面上の異なる2点(x₁,y₁)，(x₂,y₂)を通る直線の式は下記の式で表すことができる。
  • ｙ－ｙ₁＝ｙ₂－ｙ₁ｘ₂－ｘ₁(ｘ－ｘ₁)

上記の公式は二点を通る直線の式を求めるための公式です。

必須ではありませんが、覚えておくと直線の式を簡単に求めることができます。SPIは時間との勝負なので、こういった便利な公式を覚えておくことで他の人と差が開きます。