順列・組合せの練習問題を解く前にまずは、以下の内容をしっかりと熟読し、理解してから解くようにしてください。そうすることで、試験本番でもスムーズに解けるようになると思います。
SPI 『順列・組合せ』の問題の解き方
必要な知識
- 順列を求める公式
- 組み合わせ数を求める公式
『順列・組合せ』の分野は『場合の数』という分野名で言われることも多いです。このサイトでは、より内容が分かりやすいように『順列・組合せ』と表現しています。
『順列・組合せ』の問題を解くには、『順列を求める公式』と『組み合わせ数を求める公式』を知っている必要があります。
なので、『順列と組み合わせの違い』を簡単に解説した後、『順列を求める公式』と『組み合わせ数を求める公式』について詳しく解説していきます。
順列と組み合わせの違い
順列と組み合わせの違いを1~3のカードを使って解説していきます。
順列とは?
順列とは、3枚のカードから2枚を取り出す場合、取り出す順番は何通りあるか?と言ったように『順番が何通り』あるかのことです。
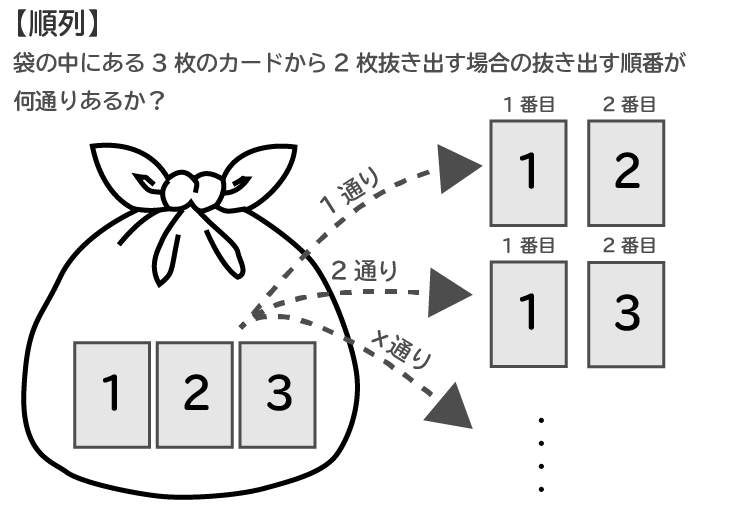
この例程度であれば、最悪、公式を忘れたとしても力業で一つ一つ出していくこともできますね。力業で出していくと、順列は全部で以下の6通りとなります。『順列を求める公式』の章で実際に公式を使って求めているので、そちらも参考にしてください。
1⇒2
1⇒3
2⇒1
2⇒3
3⇒1
3⇒2
順列は6通り。
組み合わせとは?
組み合わせとは、3枚のカードから2枚を取り出す場合、取り出す組み合わせ数は何通りあるか?と言ったように『組み合わせ数』のことです。順列との大きな違いは順番が関係ないという点です。
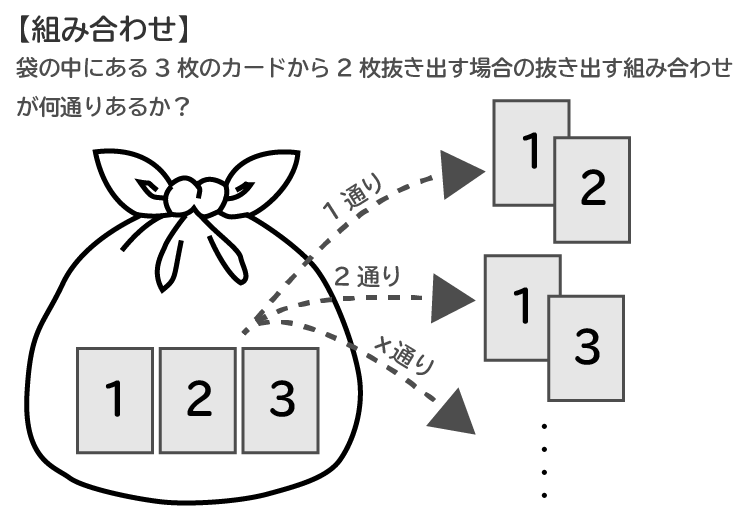
この程度であれば組み合わせ数は少ないので力業で出すこともできますが、本番で力業で出していると時間が足りなくなるので、必ず公式を使って求めるようにしてください。公式での求め方は『組み合わせ数を求める公式』の章で解説しています。
以下、力業で出した組み合わせです
1、2
1、3
2、3
組み合わせ数は3通り。
順列を求める公式

上記の公式は必ず覚えておきましょう。
先程、力業で出した『3枚のカードから2枚を取り出す場合、取り出す順番は何通りあるか?』の例を公式を使って解くと以下のようになります。
n=3
r=2
r=2なので、掛ける回数は2回だけになります。
₃P₂=3×(3-1)
=3×2
=6通り
組み合わせ数を求める公式

組み合わせを求める公式は、上記の①~④の4つあります。『順列・組み合わせ』の分野で使用するのは、主に①と②だけですが、『確率』の分野の問題で①~④全ての公式を使うので頭には入れておきましょう。
先程、力業で出した『3枚のカードから2枚を取り出す場合、取り出す組み合わせ数は何通りあるか?』の例を公式を使って解くと以下のようになります。
₃C₂=3×22×1
=3通り
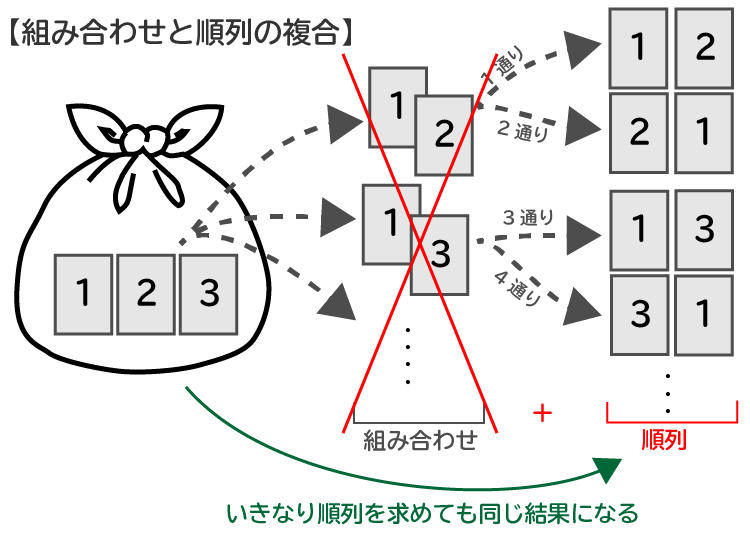
SPIでは順列と組み合わせの複合問題が出題される
実際のSPIの問題では、『順列』と『組み合わせ』の複合問題がしばしば出題されます。簡単な例を一つ紹介します。
『順列』と『組み合わせ』の複合問題
- 3枚のカードから2枚を取り出し、取り出したカードの並び順は何通りあるか?
これまでとの違い分かりますでしょうか?
一見、順列の問題のように見えますが、これは『順列』と『組み合わせ』の複合問題になります。
3枚のカードから2枚を取り出す際の取り出し順は問われていないので、この時点では単に3枚のカードから2枚を取り出す『組み合わせ数』を求めることになります。そして、2枚のカードを取り出した後に順番に並べるので、この時点で『順列』が問われています。
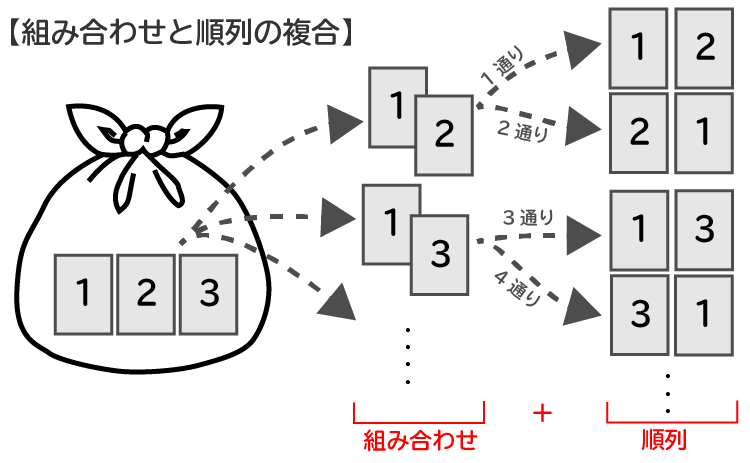
実際に問題を解いてみます。
まず、3枚のカードから2枚を取り出すので、その組み合わせ数は次の通り。
₃C₂=3×22×1
=3通り
次に抜き出した2枚のカードの並び順の通り数は、2枚のカードから2枚を取り出したことと同じなので、次のようになります。
₂P₂=2×(2-1)=2通り
3枚のカードから2枚を取り出す組み合わせ数が3通り、その各通りごとに2通りの並び順があるので、全通り数は次の通り。
3通り×2通り=6通り
よって、求める解答は6通り
勘のいい人であれば既に気が付いているかもしれませんが、問題の真面目に解くと今回のように『組み合わせ数』を求めてから『順列』を求めることになりますが、実は、今回のような問題はいきなり順列を求めても同じ結果となります。
『3枚のカードから2枚を取り出す場合、取り出す順番は何通りあるか?』
『3枚のカードから2枚を取り出し、取り出したカードの並び順は何通りあるか?』
上記の2つの問いは、同じ順列を問う問題と考えてよいということです。どちらも解答は6通りとなります。