SPI練習問題-問7(推論・論証)

SPI練習問題-問7(推論・論証)

推論(発言)に関する問題。次の設問１～設問３を解答せよ。

[設問１]下記の３つの命題が成立するとき、確実に言えることは、ア、イ、ウのどれか？

　ア：薬Ｂは薬Ｄに含まれる
　イ：薬Ａの一部は薬Ｄに含まれる
　ウ：薬Ｃは薬Ｂに含まれる

[設問２]ある学校では学期の終わりに各学級が交代で大掃除をしている。そこで、ある学級で掃除当番を決めたら次のようになった。この２つの命題から確実に言えることをア～ウの中から選べ。

　①中庭の掃除をした生徒の中には、校舎の掃除をした生徒もいる
　②体育館と校舎の両方を掃除した生徒はいない

　ア：体育館の掃除をしなかった生徒の中には、中庭の掃除をした生徒もいる
　イ：中庭の掃除をした生徒は、体育館を掃除しなかった
　ウ：体育館を掃除しなかった生徒は、校舎の掃除をした

[設問３]「スポーツ選手は、食べ物の好き嫌いが無い」「疲れやすい人は、食べ物の好き嫌いがある」を真とすると次の中で常に正しいと言えるものはどれか？

　ア：スポーツ選手は、疲れにくい
　イ：食べ物の好き嫌いがある人は、疲れやすい
　ウ：食べ物の好き嫌いがある人は、スポーツ選手ではない

解答と解説

ポイント：
待遇と三段論法は抑えておく必要がある。

待遇
「ＡならばＢである」が正しい場合、「ＢでなければＡでない」も正しいと言える。

三段論法
「ＡならばＢ」「ＢならばＣ」が正しい場合、「ＡならばＣ」も正しいと言える。

また、「～に含まれる」といった設問の場合は下図のようなベン図を描くようにしましょう。

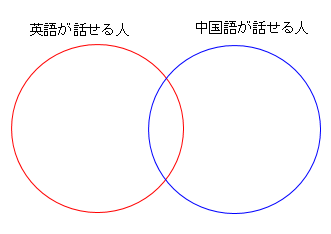
『推論・論証』の問題の解き方や、使う公式に関しては『SPI 推論・論証 ～練習問題と解き方を徹底解説！～』のページで詳しく解説しています。解き方が分からない方は、まず、そちらのページを一読してください。

設問１の解答と解説：

命題をベン図にすると下図のようになります。

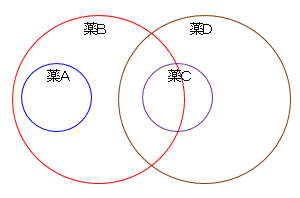
ベン図と比較しながら次にア～ウを順番に見ていきます。

ア：薬Ｂは薬Ｄに含まれる
薬Ｂの一部は、薬Ｄに含まれるが完全に含まれているわけではないので誤り。

イ：薬Ａの一部は薬Ｄに含まれる
薬Ａの一部が薬Ｄに必ずしも含まれるとは限らないので誤り。

ウ：薬Ｃは薬Ｂに含まれる
薬Ｃはの一部は、薬Ｂに含まれるが、完全に含まれるわけではないので誤り。

よって、正しいものはないので、求める解答は、Ｈとなる。

解答：Ｈ

設問２の解答と解説：

ベン図にすると下図の様になる。

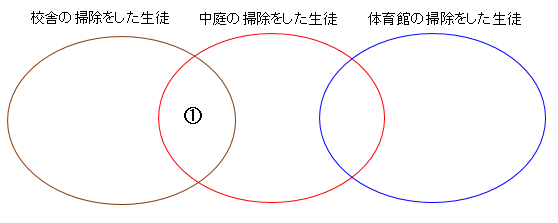
次に推論ア～ウを順に見ていきます。

ア：体育館の掃除をしなかった生徒の中には、中庭の掃除をした生徒もいる
校舎と中庭の両方を掃除した生徒の①の領域が該当する。

イ：中庭の掃除をした生徒は、体育館を掃除しなかった
必ずしもそうとは言えない。上のベン図では重なった状態にはしているが、命題では明確にされていないので、中庭の掃除をした生徒は、体育館を掃除しなかったかもしれないし、したかもしれない。よって、確実に言えないので誤り。

ウ：体育館を掃除しなかった生徒は、校舎の掃除をした
必ずしもそうとは言えない。中庭だけを掃除した生徒もいるかもしれない。

よって、正しいのはアのみで求める解答は、Ａとなる。

解答：Ａ

設問３の解答と解説：

命題より次の事が分かる。

　●スポーツ選手⇒好き嫌いが無い（命題①）
　●好き嫌いがある⇒スポーツ選手でない（命題①の待遇）
　●疲れやすい人⇒好き嫌いがある（命題②）
　●好き嫌いが無い⇒疲れにくい（命題②の待遇）

更に命題①と命題②の待遇より次の三段論法が言える

　●スポーツ選手⇒好き嫌いが無い⇒疲れにくい（命題①と命題②の待遇の三段論法）

更に命題①の待遇と命題②より次の三段論法が言える

　●疲れやすい人⇒好き嫌いがある⇒スポーツ選手でない（命題①の待遇と命題②の三段論法）

次に推論ア～ウを順に見ていきます。

ア：スポーツ選手は、疲れにくい
命題①と命題②の待遇の三段論法より、正しいと言える。

イ：食べ物の好き嫌いがある人は、疲れやすい
どの命題や命題の待遇にも該当しない。好き嫌いがある人でも疲れ難い人はいる。

ウ：食べ物の好き嫌いがある人は、スポーツ選手ではない
命題①の待遇に該当するので正しい。

よって、正しいのはアとウ。求める解答は、Ｆとなる。

解答：Ｆ