SPI練習問題-問2(順列・組合せ)
男性4人、女性5人で構成されるチームがある。この中から代表選手の3人を選びたい。男性が少なくとも1人は含まれるように選ぶとすると、その選び方は何通りあるか?
[解答群]
A 60通り
B 74通り
C 98通り
D 120通り
E いずれでもない
A 60通り
B 74通り
C 98通り
D 120通り
E いずれでもない
解答と解説
『順列・組合せ』の問題の解き方や、使う公式に関しては『SPI 順列・組合せ ~練習問題と解き方を徹底解説!~』のページで詳しく解説しています。解き方が分からない方は、まず、そちらのページを一読してください。
設問の解答と解説:
組合せが何通りあるかを求めるので、『組合せを求める公式』の方を利用します。
考え方としては次の2点を考えます。
(1)全9人から3人を選ぶ際の組み合わせ総数
(2)女性ばかりが選ばれる組み合わせ数
(1)から(2)を引くことで少なくても男性が1人以上含まれる選び方の数になります。イメージとしては、下の円グラフになります。
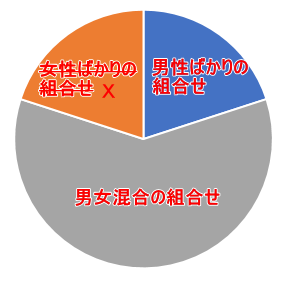
(1)全9人から3人を選ぶ際の組み合わせ総数
公式より、
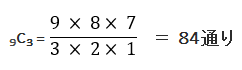
(2)女性ばかりが選ばれる組み合わせ数
公式より、
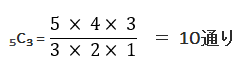
よって、求める解答は、
84通り - 10通り =74通り
解答:B




