SPI練習問題-問2(表の読み取り)
下記の様なテーブルがある。テーブルの中には、A~Fまでの6つのアルファベットが記載されています。縦1列の合計、横1列の合計が全て一致する様に各アルファベットに1~6の数字を入れる場合、A~Fの各アルファベットには何の数字が入るか?1~6の数字は1度だけ使用できる。
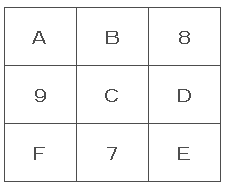
解答と解説
A~Fに1~6の数字が入るという事は、テーブルには、1~9までの9つの数字が存在することになります。この1~9の各数字を全て合計すると、45になります。
1+2+3+4+5+6+7+8+9=45
また、テーブルは、3行3列からできているという点から1行もしくは1列の合計は15(45÷3)になることがわかります。
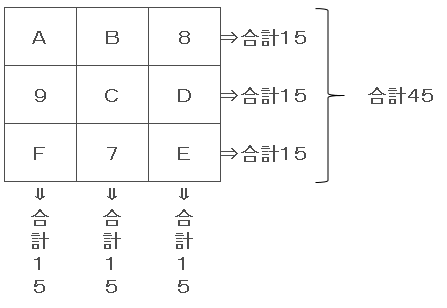
次にどれか1つのアルファベットのみに着目して見ていきます。ここではAに着目します。
1行目より
1行目の合計が15になるためには、AとBの合計が7になる必要があるので、取りうる値は、「1と6」「2と5」「3と4」になります。
Aの取りうる値:1、2、3、4、5、6 ・・・(1)
1列目より
1列目の合計が15になるためには、AとFの合計が6になる必要があるので、取りうる値は、「1と5」もしくは「2と4」になります。
Aの取りうる値:1、2、4、5 ・・・(2)
(1)(2)より、Aが取りうる値は、1、2、4、5に絞られます。あとは、ひたすら順番に当てはめていきます。
Aが1の場合、
B=6、F=5となります。
また、B=6になるのであれば、C=2となります。更に、C=2になるのであれば、D=4となります。D=4になるのであれば、E=3となります。全て1~6の数値を1回ずつ使用しているので正解になります。
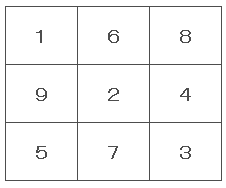
※今回の問題では、各1列、1行の合計が一致するようにとしかないので、この表は正解となりますが、斜めも見る場合は不正解となります。右下がりの合計が6になります。
Aが2の場合、
B=5、F=4となります。
また、B=5になるのであれば、C=3となります。更に、C=3になるのであれば、Dは3を入れる必要があります。しかし、Cで既に使用しているため、この組み合わせは間違いになります。
Aが4の場合、
B=3、F=2となります。
また、B=3になるのであれば、C=5となります。更に、C=5になるのであれば、D=1となります。D=1になるのであれば、E=6となります。全て1~6の数値を1回ずつ使用しているので正解になります。
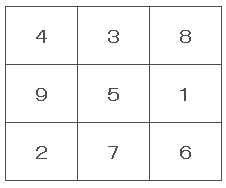
この組み合わせが、行、列だけではなく斜めも各合計15で一致するので、本来の正しい正解になります。
Aが5の場合、
B=2、F=1となります。
また、B=2になるのであれば、C=6となります。更に、C=6になるのであれば、Dは0を入れる必要があります。しかし、1~6の数値を入れなければならないので、この組み合わせは間違いになります。
よって、求める正しいテーブルの組み合わせは、下の2つになります。斜めも考慮する場合は、左の表のみが正解。






