SPI練習問題-問11(速度算)
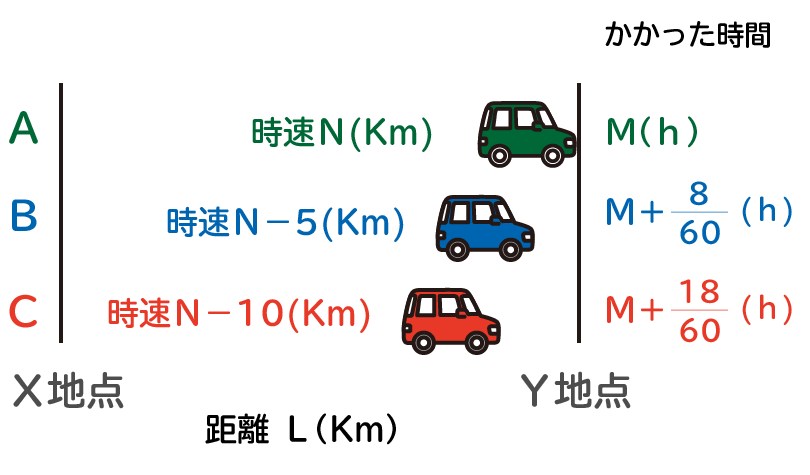
A、B、Cの3人がそれぞれの車でX地点から同時に出発してY地点に向かった。AはBより時速5Km速かったので、Bより8分速く着いた。さらにAはCより時速10Km速かったので、Cよりも18分速く着いた。
[設問1]
このとき、Bの車の速さは時速何Kmか。
A 55km/時
B 50km/時
C 45km/時
D 40km/時
E 35km/時
F いずれでもない
解答と解説
速度算の問題の解き方や、使う公式に関しては『SPI 速度算 ~練習問題と解き方を徹底解説!~』のページで詳しく解説しています。解き方が分からない方は、まず、そちらのページを一読してください。
設問1の解答と解説:
X地点からY地点までの距離をL(Km)、Aの車の速さを時速N(Km)、移動にかかった時間をM時間と仮定します。
Aの速度:時速N(Km)
XY間の距離:L(Km)
かかった時間:M(h)
今回、速さはAを基準にNと仮定しましたが、BでもCでも構いません。求めたいのがBの速さなので、Bを基準として考えるのが一般的ですが、計算が楽になるであろうところを基準とした方が、計算ミスなどが減ります。
Aの車について考える
速度が時速N(Km)、かかった時間がM(h)なので、『時間と距離と速度の公式』より、以下の式が成り立ちます。
距離 = 速度 × 時間
L=N×M ・・・(1)
Bの車について考える
BはAより時速5Km遅いので、Bの速度は次のように表すらわすことができます。
Bの速度:時速N-5(Km)
また、かかった時間はAの8分遅れで到着しているので、Aのかかった時間より8分多いことになります。ここで注意点としては時間の単位です。これまで、速度は分速ではなく時速で表されているので、分ではなく時で統一する必要があります。8分というのは、860時間なので、Bのかかった時間は次の通り。
Bの時間:M+860(h)
『時間と距離と速度の公式』より、以下の式が成り立ちます。
距離 = 速度 × 時間
L=(N-5)×(M+860) ・・・(2)
Cの車について考える
CはAより時速10Km遅いので、Cの速度は次のように表すらわすことができます。
Cの速度=Aの速度-10(Km)
=時速N-10(Km)
Cの速度:時速N-10(Km)
また、かかった時間はAより18分遅く着いたので、Aのかかった時間より18分多いことになります。ここで注意点としては時間の単位です。これまで、速度は分速ではなく時速で表されているので、分ではなく時で統一する必要があります。18分というのは、1860時間なので、Cのかかった時間は次の通り。
Cの時間:M+1860(h)
『時間と距離と速度の公式』より、以下の式が成り立ちます。
距離 = 速度 × 時間
L=(N-10)×(M+1860) ・・・(3)
Bの車の速度を求めていく
これまでの整理をすると下図のようになります。
式(1)(2)(3)ができたので、これらの連立方程式を解いていくと求めたいBの車の速度が求まります。
L=N×M ・・・(1)
L=(N-5)×(M+860) ・・・(2)
L=(N-10)×(M+1860) ・・・(3)
走った距離はいずれの車も同じなので以下の式が成り立ちます。
式(1)= 式(2)
式(1)= 式(3)
では、順に計算していきます。
式(1)= 式(2)
N×M=(N-5)×(M+860)
NM=(N-5)×(M+215)
NM=N(M+215)-5(M+215)
NM=NM+2N15-5M-23
NM-NM=2N15-5M-23
0=2N15-5M-23
0=2N-75M-10
2N-75M-10=0・・・(4)
式(1)= 式(3)
N×M=(N-10)×(M+1860)
NM=N(M+1860)-10(M+1860)
NM=NM+18N60-10M-18060
NM-NM=18N60-10M-18060
0=18N60-10M-18060
0=18N-600M-180
0=3N-100M-30
3N-100M-30=0・・・(5)
式(4)と式(5)の連立方程式を解きます。
2N-75M-10=0・・・(4)
3N-100M-30=0・・・(5)
式(4)の両辺に4、式(5)の両辺に3を掛けてMの係数を揃えます。
8N-300M-40=0・・・(4)
9N-300M-90=0・・・(5)
式(4)- 式(5)をします。
(8N-300M-40)-(9N-300M-90)=0
-N+50=0
N=50
求めたいのはBの車の速度なので、
Bの車の速度=N-5
=50-5
=45Km/h
解答:C



