SPI練習問題-問4(n進法)

SPI練習問題-問4(n進法)

２進数の足し算、引き算の問題

[設問１]１１(2)＋１０(2)の計算結果を２進数で表せ。

[設問２]１００１(2)＋１１１(2)の計算結果を２進数で表せ。

解答と解説

使用する公式：
ｎ進法の解き方に関しては、『SPI ｎ進法 ～練習問題と徹底解説！～』のページで詳しく解説しているので、参考にしてください。早く解く方法なども紹介しています。

ポイント：
表記方法に注意。数字の後ろにある(2)はその数字が２進数であることを表しています。何進数の数字なのかを明確にするためですね。今回の設問では(2)しかありませんが、１０１(10)と言った場合もあるので、パッと見で２進数だと勝手に思い込まないようにする必要があります。

２進数どうしの計算は、一旦１０進数に変換してから計算し再度、２進数に戻す方法がありますが、短時間で解くためには２進数のままで計算できるようになりましょう。

設問１の解答と解説：

２進数のままで計算する場合

　
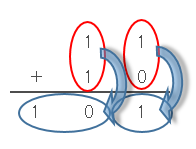
１の位の足し算は、１＋０＝１となります。１０の位の足し算は、１＋１＝１０となります。１０進数どうしの計算であれば２になるのですが、２進数どうしの計算なので、桁が繰り上がり１０となります。

よって、求める解答は、１０１．

１０進数に変換して計算する場合
２進数を１０進数に変換する場合は、２進数の一桁目から２の０乗、２の１乗、２の２乗・・・と順にかけて更に各桁を足します。

よって、２進数１１は次の通り。
　（１ｘ２¹）＋（１ｘ２⁰）
＝（１ｘ２）＋（１ｘ１）
＝ ２ ＋ １
＝ ３

２進数１０は次の通り。
　（１ｘ２¹）＋（０ｘ２⁰）
＝（１ｘ２）＋（０ｘ１）
＝ ２ ＋ ０
＝ ２

よって、２進数１１と１０を１０進数に変換すると３と２になります。このことより、１０進数どうしで足し算すると、３＋２＝５ となります。これを再度、２進数に変換する必要があります。

１０進数を２進数に変換する場合は、２で割っていきその余りを見ていきます。

よって、求める解答は１０１(2)

今回は、２進数１１や１０を１０進数に変換する際に公式を利用しましたが、２桁の２進数程度であれば１０進数でいくつになるかは頭の中で覚えておき、瞬時に出てくるようにしましょう。最低限、『2進数、8進数、10進数、16進数の対応表』は覚えておくようにしてください。

解答：Ｂ

設問２の解答と解説：

２進数のままで計算する場合
解き方は設問１と全く同様です。

２進数「１００１」と「１１１」を１の位から順に計算していきます。１の位は双方１なので「１＋１＝１０」となります。よって、計算結果の１桁目は「０」。１０の位は「０」と「１」ですが、１の位の計算で桁上がりが発生しているのでそれを加え「１＋１＋０＝１０」となり、２桁目も「０」となります。同じように１００の位、千の位も計算していくと下図のようになります。

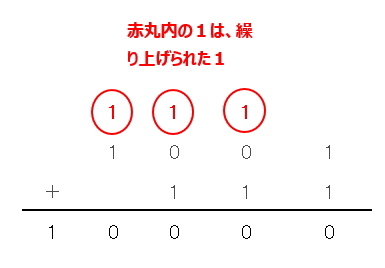
よって、求める解答は１００００(2)

１０進数に変換して計算する場合
２進数を１０進数に変換する場合は、２進数の一桁目から２の０乗、２の１乗、２の２乗・・・と順にかけて更に各桁を足します。

よって、２進数「１００１」を１０進数に変換すると次の通り。

　（１ｘ２³）＋（０ｘ２²）＋（０ｘ２¹）＋（１ｘ２⁰）
＝（１ｘ８）＋（０ｘ４）＋（０ｘ２）＋（１ｘ１）
＝８＋０＋０＋1
＝９

さらに、２進数「１１１」を１０進数に変換すると次の通り。

　（１ｘ２²）＋（１ｘ２¹）＋（１ｘ２⁰）
＝（１ｘ４）＋（１ｘ２）＋（１ｘ１）
＝４＋２＋1
＝７

よって、２進数「１００１」と「１１１」を１０進数に変換すると「９」と「７」であり、１０進数同士での足し算結果は９＋７＝１６となります。これを再び２進数に変換すると次の通り。

16(10)=10000(2)

解答：Ｉ