SPI練習問題-問1(物の流れと比率)

SPI練習問題-問1(物の流れと比率)

ある市における電気の流れを下の図に示した。Ｋ、Ｌ、Ｍ、Ｎ、Ｐ、Ｑは変電所を、s、t、u、v、wは電気の比率を表す。例えば、図では変電所Ｋから送電された電気の内、比率sがＮに送られることを示している。

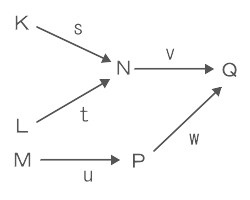
[設問１]図を表す式は、次のうちどれか？

ア　Ｑ ＝ sＫ ＋ tＬ ＋ vＮ ＋ uwＭ
イ　Ｑ ＝ svＫ ＋ tvＬ ＋ uwＭ
ウ　Ｑ ＝ v（sＫ ＋ tＬ）＋ wＰ

[設問２]図におけるそれぞれの比率は、次の通りである。

s＝0.6
t＝0.9
u＝0.5
v＝0.7
w＝0.4

変電所Ｋと変電所Ｍから送電された電気の総量が同じ場合、変電所Ｋから変電所Ｑに送られる電気量は、変電所Ｍから変電所Ｑに送られる電気量に対して、何％にあたるか？（必要な時は、最後に小数点以下第２位を四捨五入すること）

解答と解説

『物の流れと比率』の問題の解き方や、使う公式に関しては『SPI 物の流れと比率 ～練習問題と解き方を徹底解説！～』のページで詳しく解説しています。解き方が分からない方は、まず、そちらのページを一読してください。

設問１の解答と解説：

それでは、アから順番に見ていきます。

ア：Ｑ ＝ sＫ ＋ tＬ ＋ vＮ ＋ uwＭ

まず、最初に抑えて置くポイントとしては、Ｑが送電されてくるルートはＮ側からとＰ側からの２通りだということです。よって、Ｑの式は必ず次の形式になります。

Ｑ＝（Ｎ側から送られてくる送電）＋（Ｐ側から送られてくる送電）

よって、アの式は次の様に分割されます。

Ｑ＝（sＫ＋tＬ＋vＮ）＋（uwＭ）

Ｎ側から送られてくる送電は、ｖＮなので、ｓＫとｔＬは不要。よって、アは誤り。Ｐ側から送られてくる送電は、ｗＰ＝ｕｗＭ なので正しい。

イ：Ｑ ＝ svＫ ＋ tvＬ ＋ uwＭ

同様に次の式に分割されます。

Ｑ＝（sＫ＋tＬ）＋（uwＭ）

Ｎから送られてくる送電は、ｖＮ＝ｓｋ＋ｔＬに置き換えることができるので正しい。Ｐ側から送られてくる送電は、ｗＰ＝ｕｗＭ なので正しい。よって、イは正解。

ウ：Ｑ ＝ v（sＫ ＋ tＬ）＋ wＰ

Ｐ側のルートは、ｗＰなので見てすぐ正しいと分かりますね。問題は、Ｎ側のルートですが、次の式に分解することができます。

v（sＫ＋tＬ）＝ｖｓＫ＋ｖｔＬ

ｖｓＫは、Ｋから送られてくる送電量。ｖｔＬは、Ｌから送られてくる送電量を示しており正しいといえる。よって、ウは正解。

解答としては、イとウが正解なのでＦ。

解答：Ｆ

設問２の解答と解説：

変電所Ｋと変電所Ｍが送電する電気量を１００とした場合、変電所Ｋから送られてくる変電所Ｑの電気量は、

Ｑ＝１００ｘ０．６ｘ０．７
　＝４２

変電所Ｍから送られてくる変電所Ｑの電気量は、

Ｑ＝１００ｘ０．５ｘ０．４
　＝２０

よって、変電所Ｋから送られてくる電気量は、変電所Ｍから送られてくる電気量に対して

４２÷２０＝２１倍＝２１０％

と言える。よって、解答はＥ。

解答：Ｅ