SPI練習問題-問1(図形の長さと面積)
図形の面積を求める問題。下の図は、正方形と正三角形とを組み合わせた形です。
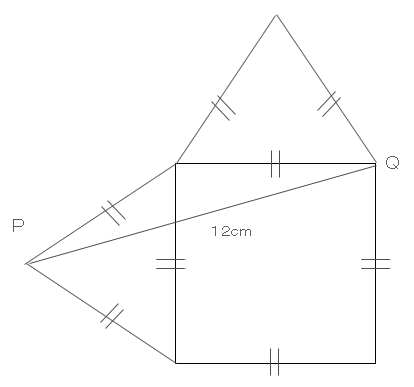
PQ=12cmのとき上の図形の面積はいくつになるか?
A 60cm²
B 72cm²
C 80cm²
D 88cm²
E 90cm²
F 92cm²
G 94cm²
H いずれでもない
解答と解説
使用する公式:
ここで、使用する公式は、平行四辺形の面積の求め方のみ。
平行四辺形の面積 = 底辺 x 高さ
あとは、気付きと発想力が非常に重要になる問題です。しかし、この手の問題は初めてやっていきなり解ける人はごく一部で、難しい、これは思いつかない、解けないと思うのは当たり前です。同類の問題を何度もやって、様々なパターンを経験しようやく解くための気付きと発想力が身に付きます。
ポイント:
面積を求めるにはどんな図形であっても底辺、高さが必要になってきます。これらが分からないと面積はまず求められません。よって、今、分かっているのは、図より線分PQの長さが12cmということだけ。よって、まずは、この線分PQの辺が底辺もしくは高さになるように図を組み替えてやる必要があります。
イメージとしては下図の様な四角形を作りたい。
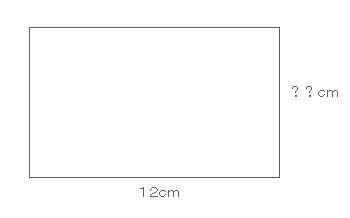
この組み換えのパターンというのが、上記でも記載した通り問題数をこなすことで直ぐに思いつくようになります。なぜなら、パターンといってもそう多くの種類は存在しないので、過去に経験していればすぐに思いつきます。しかし、逆に過去に経験したことがなければ、まず、この組み換えはすぐに思いつく人は少ないでしょう。
設問の解答と解説:
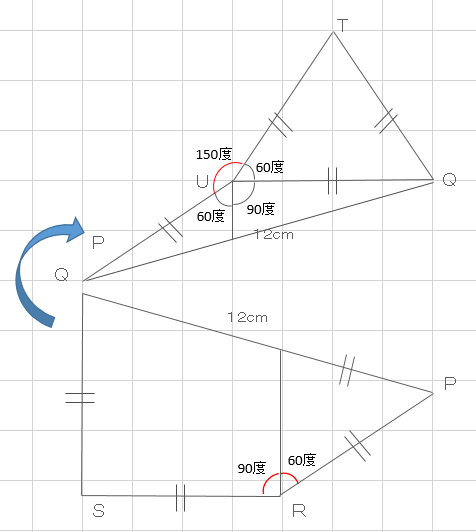
下図の様に角度を記入すると見えてくるものがあります。
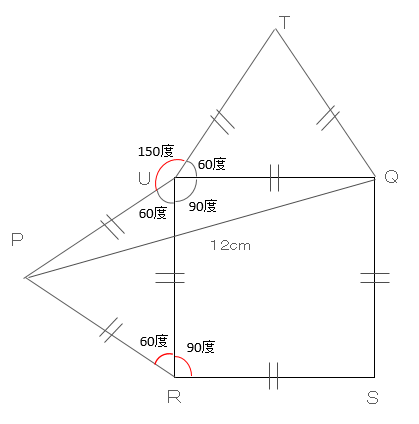
四角形の内角の総和は、360度。三角形の内角の総和は180度。よって、四角形の場合は4角あるので360度÷4角=90度。三角形の場合は、形状により1つの角の角度は変わってきますが、正三角形の場合は、全ての角が同じ角度になるので、180度÷3角=60度となる。
手順1:
線分PU、UT、PR、RSはすべて同じ長さ。更に角PUTと各PRSの赤線側の角度はいずれも150度となります。よって、辺PUTと編PRSは角度も長さま同じなのでピッタリくっつくことが分かります。
そこで、線分PQを境に図形を分割させます。更に分割させた下側の図形PQSRを左右反転させます。
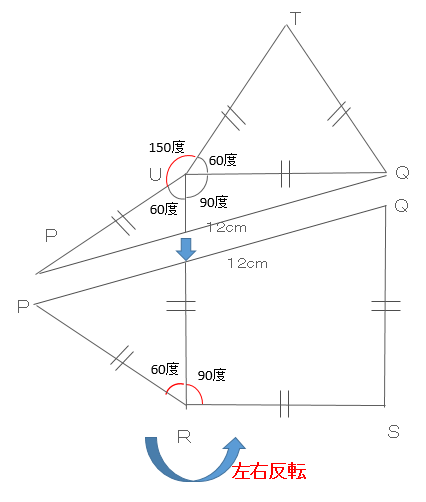
手順2:
図形PQSRを左右反転させると下図のようになります。そして更に図形PQSRを時計回りにぐるっと回転させます。
手順3:
図形PQSRを時計回りにぐるっと回転させると下図のように2つの図形がぴったりくっつき四角形ができます。更に、線分QSと線分PQは同じ長さ。また、残りの2辺も元々は同じ線分PQで12cmで等しいよって、それぞれの向かい合う辺の長さが同じということは、四角形もしくは平行四辺形ということになる。
しかし、角Qは75度なのでこの図形は四角形ではなく平行四辺形ということがわかる。
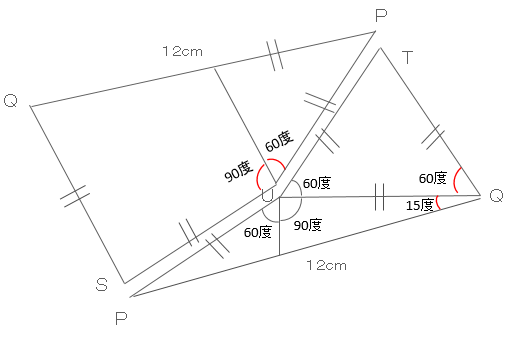
三角形P(S)-U-Qの角Uが150度なので、残りの2角の合計は30度となる。この三角形は二等辺三角形なのでそれぞれの角度は15度だと分かる。また、三角形P(T)-U-Qは正三角形なのでそれぞれの角度は60度。よって、角Qは75度となる
手順4:
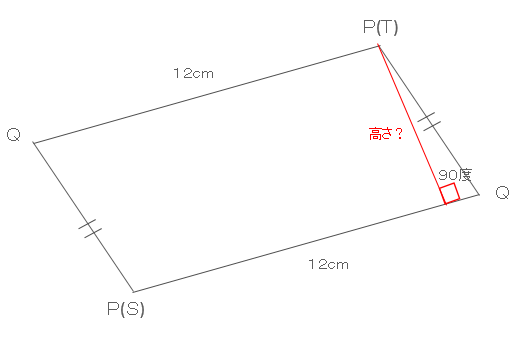
手順3で平行四辺形が出来上がり、求める面積は、底辺x高さになる。しかし、底辺は12cmと判明しているが、高さが現時点で分からない。手順3で作成した平行四辺形の余分な線を取っ払いシンプルにしたのが下図になります。求めたいのは、赤線の高さ。
ここで、元の図形に戻って少し見てみたいと思います。下図の元の図形に線分TSを引きます。線分TSは、線分PQと全く同じ長さになるので12cmになります。
更に下図の三角形TQSの②③④の合計角度が150度となり残りの2角の合計が30度となります。よって、①が15度になります。また、①②③の合計が90度ということより、⑤が90度になることが分かります。
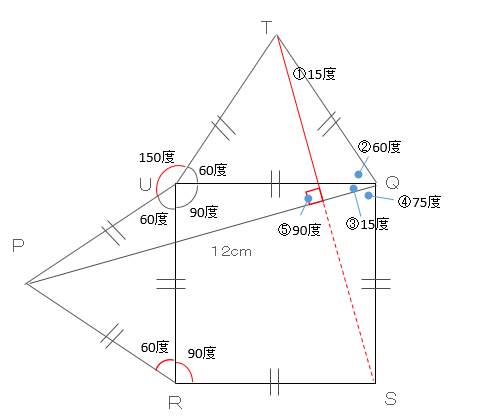
このことより、上図の赤色の実線部分が平行四辺形の高さの線と同じだという事も分かります。また、⑤が90度ということより、赤色の実線と、赤色の点線は全く同じ長さで線分TSを2等分していることが分かります。
よって、赤色実践(高さ)は12÷2=6cmになります。
したがって、求める解答は、12cm(底辺)x 6cm(高さ)= 72cm²
解答:B


