SPI練習問題-問11(仕事算・水槽算)

仕事算に関する問題。次の設問を答えよ。

[設問１]Aが仕事を6日間をした後にAに代わってBが残りの仕事を10日間で終わらした。この仕事を初めからAとB二人が同時に行うと何日間で完了しますか。AとBが一日で行う仕事量の比は4:5である。

[解答群]
Ａ　6日目
Ｂ　7日目
Ｃ　8日目
Ｄ　9日目
Ｅ　10日目
Ｆ　11日目
Ｇ　12日目
Ｈ　いずれでもない



解答と解説

必要な知識：
仕事算・水槽算の問題を解く場合、全体の仕事量を１と仮定して計算するのが基本です。ただし、必ずしも１と仮定する必要はなく、１人で仕事をした場合にかかる各々の日数の最小公倍数を全体の仕事量と仮定した方が計算が簡単になる場合が多いです。

仕事算・水槽算の解き方や、上記の仕事量の仮定値の設定方法が分からない方は、『仕事算・水槽算 ～練習問題と解き方を徹底解説！～』のページで詳しく解説しているので、そちらを参考にしてください。

設問１の解答と解説：

AとBが一日で行う仕事量の比が4:5ということは次のことが言えます。

　A：B ＝ 4：5

　仕事算

これは、Aが行う仕事量をBであれば4/5の時間(80％の時間)で終わらせることができることを意味します。逆に、Bが行う仕事量をAがやろうと思うと、5/4の時間(125％)かかることを意味しています。

今回の仕事は、Aが6日間、Bが10日間行っています。

もし、Bの10日間をAが実施した場合、10×5/4＝50/4日間(12.5日)かかることになります。よって、この作業全体をAが1人で行った場合は、A自身が元々実施した作業時間の6日間も加え次の通りになる。

　Aが1人で作業した場合にかかる日数 ＝ 6日 + 50/4日 ＝ 74/4 日(18.5日)

作業全体で74/4 日(18.5日)かかるので、作業量全体を1とした場合、1日あたりのAの作業量は、1/18.5 になります。小数が分母になると後々計算が面倒なのでここはあえて分数で計算しておきます。

　仕事算

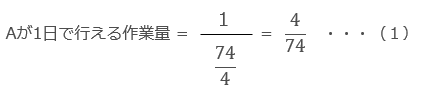
同様の考えで、Aが実施した6日間をBが実施すると、4/5の期間で終わらすことができるので、6 × 4/5 ＝ 24/5(4.8日)で終わらせられる。よって、この作業全体をBが1人で行った場合は、B自身が元々実施した作業時間の10日間も加え次の通りになる。

　Bが1人で作業した場合にかかる日数 ＝ 10日 + 24/5日 ＝ 74/5 日(14.8日)

作業全体で74/5 日(14.8日)かかるので、作業量全体を1とした場合、1日あたりのAの作業量は、1/14.8 になります。

　仕事算

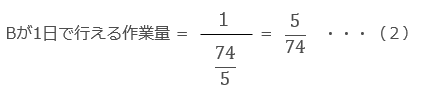
これで、Ａの1日で行える作業量(１)とBが1日で行える作業量（２）がでました。この（１）と（２）を合計した数値が、AとBの2人が一緒に作業してできる1日の作業量になります。

　AとBが一緒に作業した場合、1日でできる作業量 ＝ 5/74 + 4/74 ＝ 9/74

2人での1日の作業量ができました。この作業を何日間か続けて行い、全体の作業量1が完了すればいいわけです。求めたいかかる日数をＮとした場合、また、作業量全体を1としているので、次の式が成り立ちます。

　9/74 × Ｎ ＝ 1
　Ｎ ＝ 74/9 ＝ 8.222

よって、全体の作業量1を終わらせるためには、8.2222～日間かかることになります。8.2222～日というのは、8日目では終わらず、9日目に入っていることになります。したがって、もとめる解答は、9日目。

解答：Ｄ