4辺の長さが等しい平行四辺形A、B、C、Dがあります。各辺の中点を、E、F、G、Hとし対角線ACと４辺の長さは等しいものとします。

q9-1

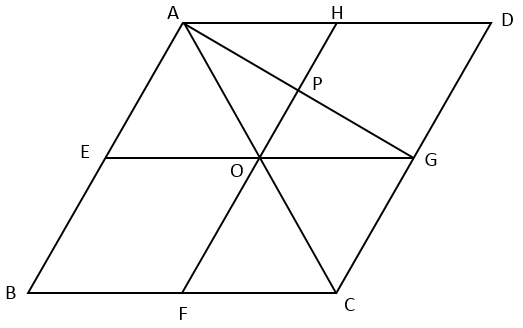
このとき、次の設問に答えよ。

[設問１]正三角形はいくつありますか？
[設問2]二等辺三角形はいくつありますか？

解答と解説

事前準備：
まずは、平行四辺形ABCDに含まれる三角形を全て抽出します。その結果、次の11個の三角形が見つかります。これら11個の三角形を「正三角形」「二等辺三角形」「それ以外」に分類していくことで設問の回答を求めることができます。

　(1) 三角形ABC
　(2) 三角形ACD
　(3) 三角形AEO
　(4) 三角形OFC
　(5) 三角形ACG
　(6) 三角形AOP
　(7) 三角形AOG
　(8) 三角形POG
　(9) 三角形AGD
　(10) 三角形APH
　(11) 三角形OCG
　(12) 三角形AOH
　(13) 三角形AEG

設問１解説：
それでは、三角形(1)～(11)を順に見ていきます。

(1) 三角形ABC
設問より辺ACは、平行四辺形の4辺と長さが等しいということなので、「AB＝BC＝AC」になります。よって、三角形ABCは、正三角形。

(2) 三角形ACD
(1)と同様。「AD＝CD＝AC」になります。よって、三角形ACDは、正三角形。

(3) 三角形AEO
E点は、辺ABの中点なので、辺AEの長さは辺ABの半分。同様に辺EOの長さも辺BCの長さの半分。更に辺AOも辺ACの長さの半分。よって、三角形AEOは、(1)三角形ABCの各辺を1/2スケールにしただけの三角形。

したがって、三角形AEOは、正三角形。

別の求め方として、角度で考えてもいい。

三角形ABCは正三角形なので、∠BAC＝∠ABC＝∠BCA＝60° だと分かる。更に辺EOと辺BCは並行なので、∠AEO＝∠ABC＝60°、∠AOE＝∠ACB＝60° となる。

よって、三角形AEOの3つの内角はいずれも60°なので正三角形と分かる。

(4) 三角形OFC
(3)三角形AEOと同様の考え方。三角形OFCは、(1)三角形ABCの各辺を1/2スケールにしただけの三角形。

したがって、三角形OFCは、正三角形。

(5) 三角形ACG
三角形ACDは正三角形なので∠ACG＝60°とすぐに分かる。更に辺AGは、∠CADを2等分しているので∠CAG＝30° となる。よって、残る∠AGCは、180-60-30＝90°。

したがって、三角形ACGの3つの内角は全てバラバラなので、正三角形でも2等辺三角形でもない。

(6) 三角形AOP
(5)三角形ACGと同様。三角形AOPは、(5)三角形ACGの各辺の長さを全て1/2したサイズ。よって、三角形AOPの3つの各内角は、(5)三角形ACGと同じ、60°、30°、90°となり、バラバラ。

したがって、三角形AOPは、正三角形でも2等辺三角形でもない。

(7) 三角形AOG
辺AOは、辺ACの半分の長さ。辺OGは、辺EGの半分の長さ。辺ACと辺EGの長さは等しいので、辺AOと辺OGの長さも等しいと言える。更に∠OAGは、30°なので、三角形AOGが正三角形でないことは明らか(正三角形の場合は、各3つの内角はそれぞれ60°となる)。

したがって、三角形AOGは、2等辺三角形。

(8) 三角形POG
∠POGは、∠ABCと同じ。よって、∠POG＝60°。更に三角形AOGは(7)より辺OAと辺OGが等しい2等辺三角形でかつ、∠OAG＝30°と分かっている。よって、∠OGAも30°となる。

このことより、残る∠OPGは、180-60-30＝90° となり、三角形POGの各内角はそれぞれ60°、30°、90°となり、バラバラ。

したがって、三角形POGは、正三角形でも2等辺三角形でもない。

(9) 三角形AGD
考え方は、(5)三角形ACGと同じ。
辺AGは、∠CADを二等分しているので、∠GAD＝30°。∠ADG＝60°なので、残る∠AGDは、180-30-60＝90°。三角形AGDの各内角はそれぞれ60°、30°、90°となり、バラバラ。

したがって、三角形AGDは、正三角形でも2等辺三角形でもない。

(10) 三角形APH
三角形APHは、三角形AGDの各辺を1/2しただけの三角形。よって、各内角はそれぞれ60°、30°、90°となり、バラバラ。

したがって、三角形APHは、正三角形でも2等辺三角形でもない。

(11) 三角形OCG
三角形OCGは、三角形ACDの各辺を2等分しただけの三角形。三角形ACDは正三角形なので、三角形OCGも正三角形だとわかる。

よって、三角形OCGは、正三角形。

(12) 三角形AOH
三角形AOHは、三角形ACDの各辺を2等分しただけの三角形。三角形ACDは正三角形なので、三角形AOHも正三角形だとわかる。

よって、三角形AOHは、正三角形。

(13) 三角形AEG
三角形AEGと三角形POGは2組の内角が等しいので相似な三角形になります。三角形POGは(8)より、正三角形でも2等辺三角形でもないことが分かっています。

したがって、三角形AEGは、正三角形でも2等辺三角形でもない。

これらより、正三角形、二等辺三角形、どちらでもない三角形の数は次の通りになる。

　正三角形は、6つ
　二等辺三角形は、1つ
　どちらでもないは、6つ

よって、求める解答は、6つ。

解答：6つ

設問２解説：
設問１より、求める解答は、1つ。

解答：1つ