設問1
下記の小数計算を解くと結果はいくつになるか?
設問2
下記の分数計算を解くと結果はいくつになるか?
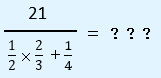
設問3
下記の方程式を解くとXはいくつになるか?
設問4
下記の2次方程式を解くとXはいくつになるか?
解説と解答
■設問1の解説と解答
足し算より、掛け算、割り算を優先的に計算する必要があるので、設問1の場合であれば()内を先に計算しなければなりません。
(0.4 ÷ 0.8) + (0.2 x 2.8)
()内を計算すると、次のようになります。
0.5 + 0.56 = 1.06
よって、解答は1.06となります。ここで、小数同士の掛け算ならともかく割り算は難しい。「0.4 ÷ 0.8」がすぐに計算できないという人は、小数を整数に変えて計算することができます。例えば、小数に10を掛けると一桁繰り上がり、0.4であれば、4に。0.8であれば8になります。
しかし、ここで注意点があります。10を掛けたら一桁繰り上がって整数にできるからといって下記のように単純に10を掛けてはいけません。単純に10を掛けてしまうと、数字が10倍されることになるので、元の数値とは全く別物になってしまいます。
(0.4 ÷ 0.8 x 10) + (0.2 x 2.8) ⇒ やってはダメ!
では、どうすればいいのか?設問の式の割り算部分を分数に置き換えると下記のようになります。
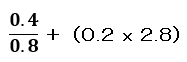
そして、10を掛ける場合は、分母と分子の両方に10を掛ける必要があります。そうすると、10/10 は約分すると1になるので1を掛けているのと同じことになり数字が別物になってしまうことはありません。。
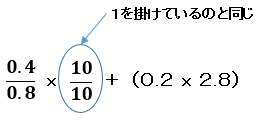
計算すると下記のようになります。
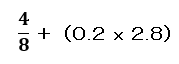
0.5 + 0.56 = 1.06
■設問2の解説と解答
分数の分母が更に分数になっている場合は、まずは分母の分数から計算するようにしましょう。今回の設問であれば、下記の部分ですね。
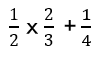
計算すると、7/12となります。
![]()
よって、分母が7/12なので、
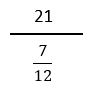
となります。そして、最後に分母と分子の両方に12/7を掛けて分母を無くしてしまいます。
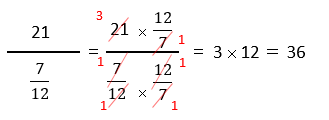
よって、求める答えは、36となります。
■設問3の解説と解答
まずは、右辺(=の右側)の()を外してやります。
6000(-3+x)= 6000x(-3)+ 6000x = -18000 + 6000x
よって、右辺の()を外すと -18000 + 6000x となります。これを元の式に戻すと次の式になります。
4000x - 12000 = -18000 + 6000x
次に、x付きの数値と、なしの数値どうしを計算するために、x付きの数値を右辺に、なしの数値を左辺に移行してやります。
18000 - 12000 = 6000x - 4000x
これを計算すると、下記のようになります。
6000 = 2000x
ここからxを求めると、
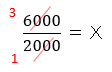
となり、求める解答は X=3 となります。
■設問4の解説と解答
まずは、右辺の数字をすべて左辺に移行します。
![]()
そして、左辺の計算できるところは、計算してしまいましょう。
![]()
次に因数分解をする必要があります。たすき掛けなどを使用して因数分解をすることもできますが、この程度の2次方程式の場合は、使用しない方が簡単でしょう。因数分解の方法は、そして、覚えるしかありません。
因数分解の方法は、
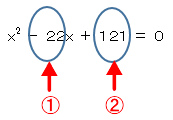
①足して-22となる二つの数値
②掛けて121となる二つの数値
上の①②の両方を満たしている二つの数値を探します。慣れてくると簡単に分かるのですが、慣れてないとなかなか出てこないかもしれませんね。
この二つの数値は、-11と-11です。-11と-11を足すと、-22になります。更に-11と-11を掛けると121になりますね。よって、因数分解すると下記のようになります。
(x-11)(x-11)= 0
![]()
よって、求める解答は X = 11 となります。


