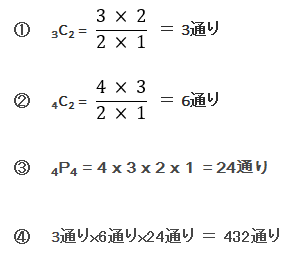SPI練習問題-問1(順列・組合せ)

SPI練習問題-問1(順列・組合せ)

大人３人、子供４人がいる。ここから４人を選んでリレーチームを作りたい。

[設問１]走る順番は何通りあるか？

[設問２]大人２人、子供２人を選ぶとき、走る順番は何通りあるか？

解答と解説

『順列・組合せ』の問題の解き方や、使う公式に関しては『SPI 順列・組合せ ～練習問題と解き方を徹底解説！～』のページで詳しく解説しています。解き方が分からない方は、まず、そちらのページを一読してください。

設問１の解答と解説：

ここは素直に公式を使うのが確実で一番早い。順列と組合せの公式がごっちゃにならないように覚えましょう。設問１は、『走る順番は何通りあるか？』を問われているので順列の公式を使います。

ｎは、大人３人と子供４人の合計７人となります。
ｒは、合計７人の中から４人を選択するので、４人となります。

解答：Ｃ

設問２の解答と解説：

設問１と同じく『走る順番は何通りあるか？』を問われているので順列だなと思ってしまい勝ちですが、組合せと順列の両方を使う必要があります。そして、次の４つの計算から最終的な解答を出さなければなりません。

①大人３人の中から２人を選ぶ組合せの数
②子供４人の中から２人を選ぶ組合せの数
③選んだ４人の並び順の数
④最後に①②③をの数を掛けた結果が、走る順番の総数になります。

え？③が解答になるのではないの？と思われる方もいるかもしれませんが、③で算出した数はあくまで７人の中から選んだ４人１パターンに対する並び順の数になります。４人の組合せパターンは全部で①ｘ②のパターン数だけあります。

よって、全パターンに対する走る順番の数は、①ｘ②ｘ③となります。

解答：Ｃ