
図形の長さと面積 練習問題集
図形の長さと面積の練習問題を解く前にまずは、以下の内容をしっかりと熟読し、理解してから解くようにしてください。そうすることで、試験本番でもスムーズに解けるようになると思います。
SPI 図形の長さと面積の問題の解き方
重要なポイント
- 多くの練習問題を解き、パターンを知る
- 公式や図形の持つ性質を頭に入れておく
公式さえ覚えておけばいいと思っていませんか?
SPIの『図形の長さと面積』の問題を解くには上記の2点が非常に重要です。どちらか一方が欠けると、解けなかったり解くのに時間がかかってしまいます。SPIで1問解くのに5分以上かかると例え解けたとしても他の問題を解く時間が無くなり、致命的になってしまいます。
自分は公式が頭に入っているから大丈夫と思っている方、是非、『練習問題1』をやってみてください。恐らく解説を見ないと解けないと思います。解けたとしても5分以上かかると思います。
『図形の長さと面積』の問題は多くの問題数をこなし、様々なパターンを知っておく必要があります。そうすることで、本番では『あぁ、あの方法を使えば解けるね』と瞬時に解き方が頭に浮かんでくるようになります。
覚えておくべき公式
重要な公式
- 円の面積=半径×半径×π
- 扇形の面積=半径×半径×π×中心角÷360
- 三角形の面積=底辺×高さ÷2
- 四角形の面積=底辺×高さ
- 平行四辺形の面積=底辺×高さ
- 円周の長さ=直径×π
SPIの『図形の長さと面積』で出題される問題を解くには最低限、上記の知識は頭に入れておく必要があります。数は多いですがいずれも一般的な知識なので、ほとんどの人が既に頭に入っているかと思います。
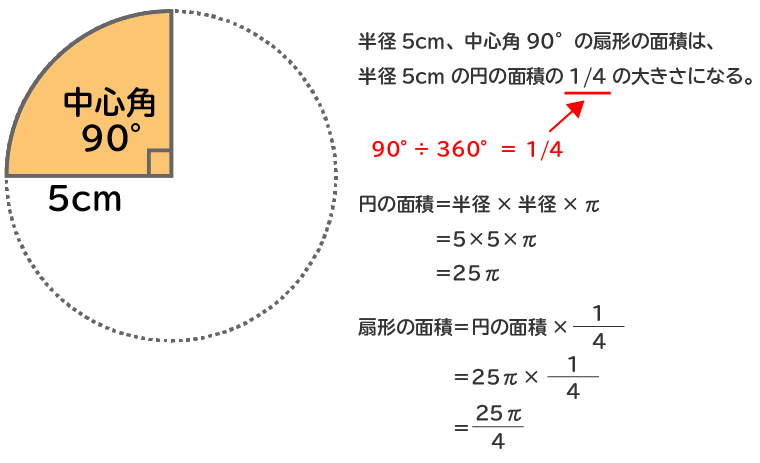
扇形の面積は少し複雑ですが、円の面積の求め方を知っていれば、忘れたとしてもそこから答えを出すことができます。
知っておくべき図形の持つ性質
SPIの『図形の長さと面積』の問題は、公式を覚えておくだけではなく以下のような図形の持つ性質も知っておく必要があります。
図形の持つ性質
- 三角形の内角の和=180°
- 四角形の内角の和=360°
- 対頂角は等しい
- 平行な2直線の同位角、錯角は等しい
- 平行な2直線の同側内角の和=180°
この他にも図形の持つ性質はたくさんあります。三角形の合同条件や相似条件なども知っておくと効率的に問題を解けるようになります。

