SPI練習問題-問1(分割払い)

SPI練習問題-問1(分割払い)

分割払いに関する問題。

[設問１]車を１２回の分割払いで購入した。初回は、車の代金全体の９分の１支払い、２回目以降は初回支払い後の残額を均等割して支払うことになった。２回目の支払い額は車の代金全体のどれだけにあたるか？

[設問２]新しいソファーを購入した。支払いは１０回の分割払いとし、購入日に１回目の支払いとして全体の7分の１を支払い、２回目以降は均等に支払うことにした。４回目の支払い額は総額のどれだけにあたるか？

解答と解説

用語に関して：
分割払いとは：借入金を一括ではなく数回に分割して支払うこと。
均等払いとは：分割払いをするさいの、分割方法のこと。

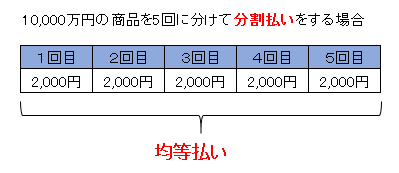
分割払いは、１万円の商品を購入した際に一括で支払うのではなく数回に分けて支払う事を言う。また、分割払いの分割方法は、様々で最初の数回を多めに払い、徐々に支払い額を減らしていく方法や、毎回均等の額を返済する均等払いなどがある。

『分割払い』の問題の解き方や、使う公式に関しては『SPI 分割払い ～練習問題と解き方を徹底解説！～』のページで詳しく解説しています。解き方が分からない方は、まず、そちらのページを一読してください。

設問１の解答と解説：

支払い方法のイメージは下図のようになります。最初の１回目の支払いは車の代金総額の１/９を支払う。残りの８/９の金額は、残り１１回で均等に分割して支払う。

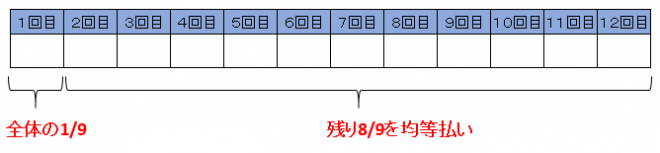
よって、残金８/９を１１回に均等に分けて支払うので１回当たりの支払う額は、８/９を１１で割った額になります。

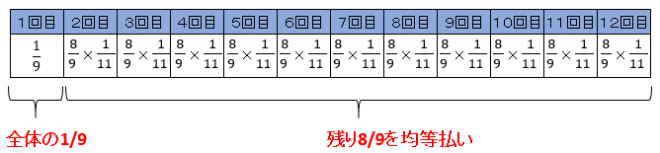
よって、２回目の支払い額は、全体の（８/９）ｘ（１/１１）＝８/９９となります。

解答：Ｂ

設問２の解答と解説：

考え方は、設問１と同じ。１回目で全額の１/７を支払い、残り９回で残額６/７を均等払いで返済します。よって、２回目以降の各回の支払は、残額６/７を９で割った額になります。

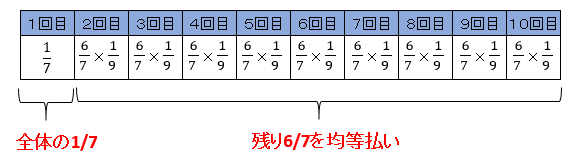
　（６/７）ｘ（１/９）＝ ６/６３ ＝ ２/２１

よって、４回目の支払額は総額の２/２１となり、Ｃが正しい。

※補足
もし、設問の内容が４回目までに支払った額が総額のどれだけにあたるか？という場合は、１回目～４回目までの額を合計します。

（１/７）＋（２/２１）＋（２/２１）＋（２/２１）＝ ９/２１ ＝ ３/７

解答：Ｃ