一次方程式は次の式で表されます。
そして、『aは傾き』、『bは切片』と呼ばれています。実際にグラフで表現されるときには、下記の例の様にaとbには具体的な数値が入ります。
(例)
y=2x+2
y=-3x+2
では、aの傾き、bの切片とは一体何を意味するのか? これは、グラフを見た方が分かり易いのでグラフを用いて説明致します。
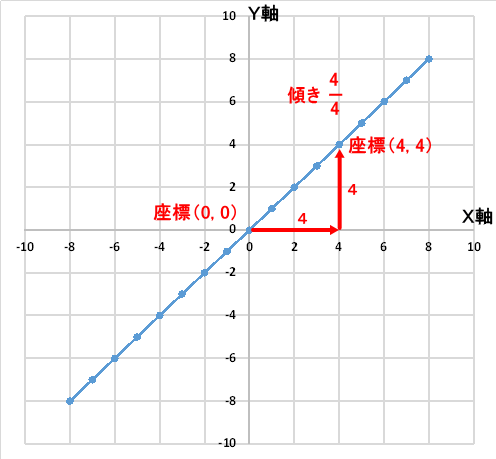
傾きaはグラフの傾きを表します。そしてその傾きaは,X軸の正の向きに1目盛り進んだときにY軸の方向にに幾ら進むかを表したものです。ここでX軸の正の向きに1目盛りと書きましたが、1目盛りにこだわる必要はありません。X軸1目盛り進んだ時のY軸の値が読み取り難い場合は、読み取り易い場所を見つけてもらって結構です。
例えば上のグラフであれば、X軸方向に4目盛り進んだとき、Y軸方向にも4進んでいるのがわかります。座標で言うと、(0, 0)から(4, 4)に進んでいます。
座標は、(X座標, Y座標)で表されます。
そして傾きaは次の式で表されます。

よって、上のグラフの傾きは、1となります。
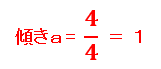
次に切片bですが、切片bは、グラフとY軸のが交わるY座標になります。
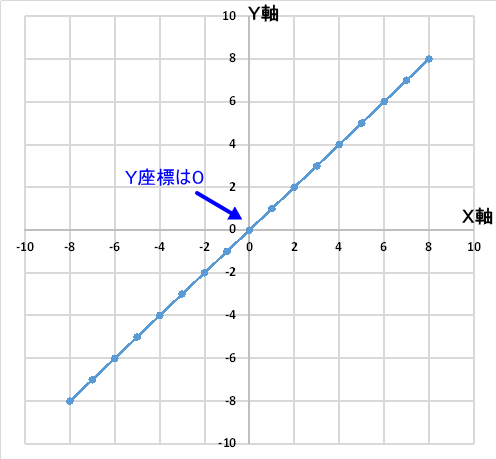
上のグラフであれば、Y座標が0のところでグラフとY軸が交わっています。よって、切片bは0となります。
これらより、このグラフのy=ax+bの一次方程式は、
y=1x+0
で表されます。当然、1や0は省略されるので、
y=x
がこのグラフの一次方程式となります。
これは最もシンプルなグラフなのでもう少し例を記載したいと思います。
一次方程式の右上がりグラフの例
上の様なグラフの場合の一次方程式はどうなるでしょうか?
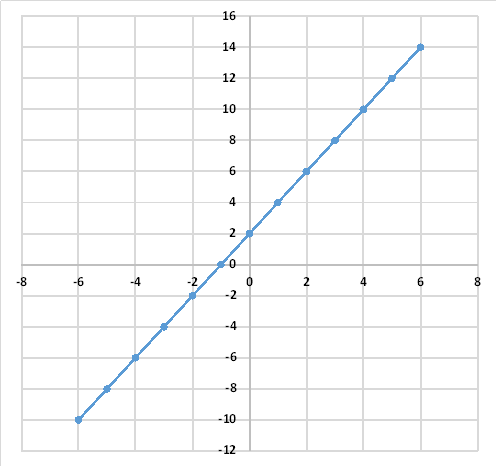
まずは、先程と同じようにグラフから傾きaと切片bを求めます。傾きaは下の図のようにX軸方向に0から2へ2移動するとY軸方向は2から6へ4移動しています。よって、傾きaは、2となります。
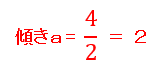
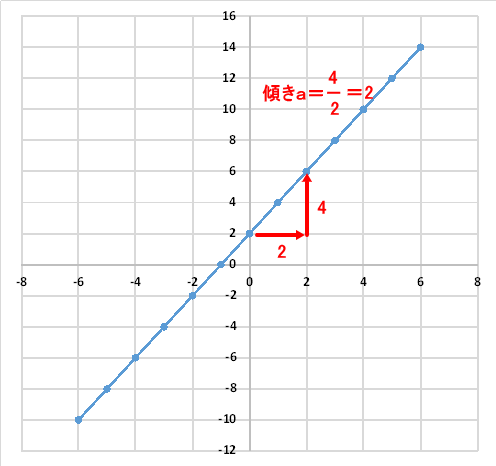
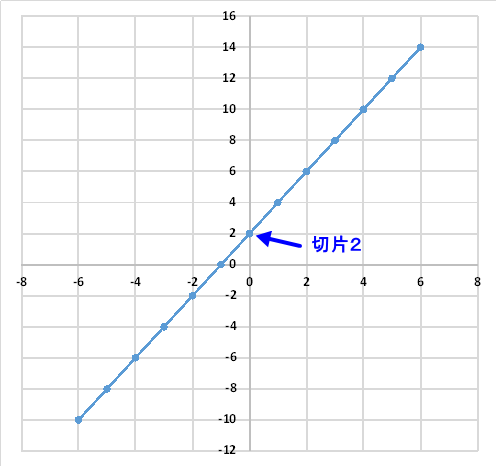
次に切片bですが、下図の様にグラフとY軸はY座標2で交わっています。よって、切片bは、2となります。
よって、このグラフの一次方程式は、
y=2x+2
となります。
一次方程式の右下がりグラフの例
次に下のグラフの様に右下がりのグラフの場合、一次方程式がどのようになるかを見てみたいと思います。
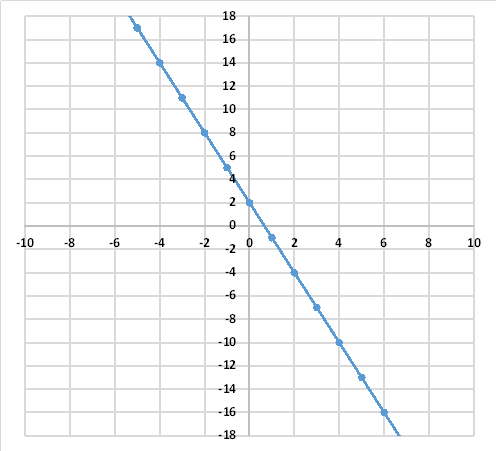
傾きaと切片bの求め方は基本的には右上がりのグラフと同じです。まずは、傾きaを見てみます。X座標0から2へX軸方向に2目盛り進むと、Y座標は、2から-4へ-6目盛り移動していることがわかります。
よって、グラフの傾きは、-3となります。
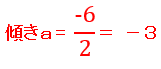
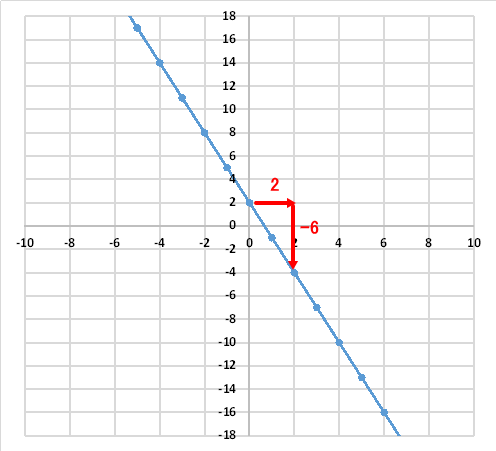
傾きaを求めるさいにX座標とY座標の移動目盛り量を読み取るのですが、目盛りが読み取り易い場所で読み取ってもらって結構です。例えば下図のようにX座標が2から4へ2目盛り移動した際にY座標は-4から-10へ-6目盛り移動するでも結構です。
結果としては、X軸方向に2目盛り、Y軸方向に-6目盛り移動したことになり、同じ傾きの-3になります。
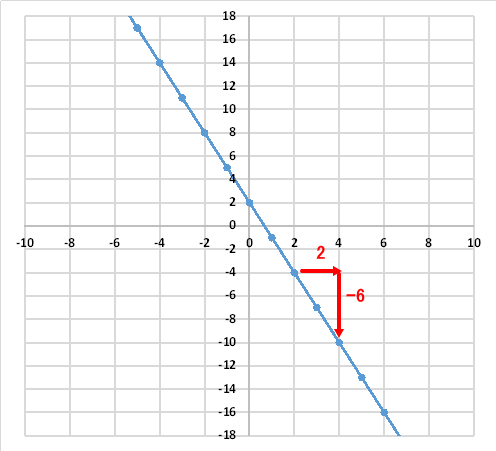
次に切片bですが、Y軸と交わっているY座標は、2なので、このグラフの一次方程式は次のようになります。
y=-3x+2
このように、右下がりのグラフは、X軸が正の方向に動いた際にY座標がマイナス方向に動くので、傾きaがマイナスの一次方程式になります。逆に右上がりのグラフは、X軸が正の方向に動いた際にY座標がプラス方向に動くので、傾きaがプラスの一次方程式になります。
傾きaと切片bが分かっているグラフの書き方
これまではグラフから傾きaと切片bを読み取り、一次方程式をもとめていましたが、今度は逆に一次方程式からグラフを描く方法を記載します。下の一次方程式はどのようなグラフになるでしょうか?
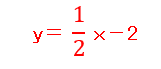
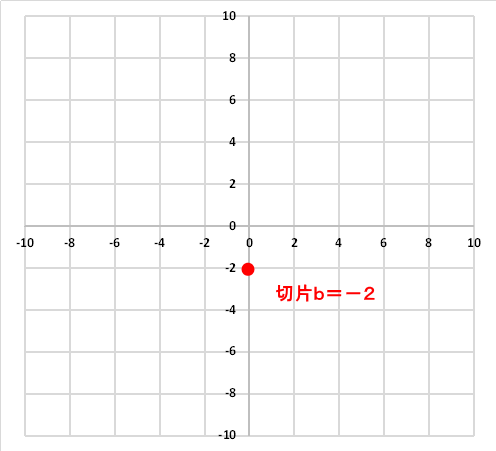
一次方程式より、傾きaが1/2。切片bが-2 だという事がわかります。切片bはY軸との交点でしたよね。よって、まずは切片bのY座標が2になる場所をプロットします。
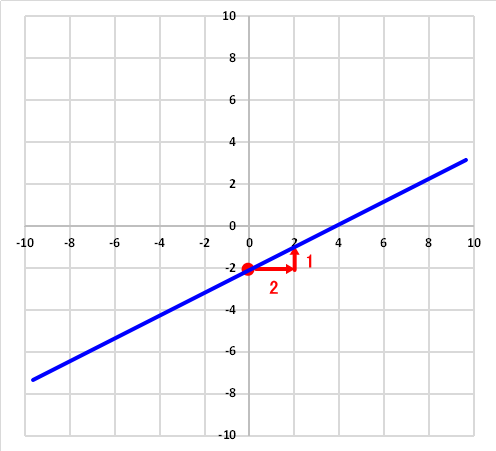
次に傾きは、X座標の移動目盛り量とY座標の移動目盛り量なので切片bからその目盛り量を移動します。傾きaが1/2ということは、Xの正方向に2目盛り移動した場合、Y座標は1移動することになります。
その移動した点と、切片を結べば一次方程式のグラフが完成します。
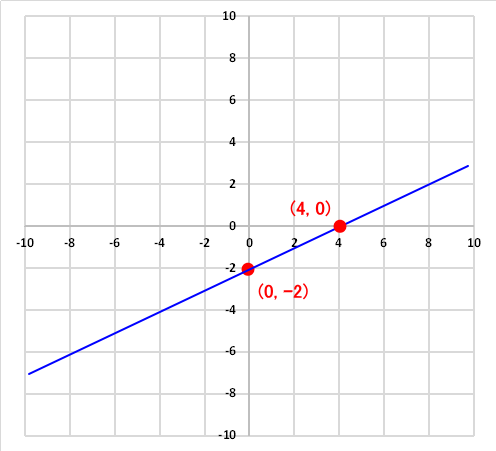
一次方程式y=1/2x-2 に実際に任意の何らかの値を入れてグラフを描く方法もあります。
例えば、x=0 のとき一次方程式にx=0を代入するとy=-2となります。よって、このグラフは、座標(0, -2)を通ることが分かります。更に任意のもう1点を求めます。x=4とした場合、一次方程式に値を代入するとy=0 となります。よって、このグラフは座標(4, 0)も通ることが分かります。この2点を線で結んだグラフが一次方程式のグラフになります。
グラフとしては同じものができるはずです。