SPI練習問題-問1(集合)
ある地域の中学生300人を対象に、季節とスポーツについてのアンケートを行った。下の表はその結果の一部である。
| 質問 | 解答 |
|---|---|
| 夏が好きか | 好き 240人 きらい 60人 |
| 水泳が得意か | 得意 180人 得意ではない 120人 |
| 冬が好きか | 好き 270人 きらい 30人 |
| スキーが得意か | 得意 210人 得意ではない 90人 |
[設問1]夏が好きで、かつ水泳が得意だと答えた人が150人いた。夏がきらいで、かつ水泳が得意ではないと答えた人は何人か?
A 20人
B 30人
C 50人
D 60人
E 70
F いずれでもない
[設問2]夏も冬もきらいだと答えた人が10人いた。夏と冬のいずれか一方だけを好きと答えた人は何人か?
A 50人
B 60人
C 70人
D 90人
E 120人
F いずれでもない
[設問3]水泳もスキーも得意ではないと答えた人が50人いた。水泳かスキーの少なくとも1つは得意だと答えた人は何人か?
A 220人
B 230人
C 240人
D 250人
E 260人
F いずれでもない
解答と解説
『集合』の問題の解き方や、使う公式に関しては『SPI 集合 ~練習問題と解き方を徹底解説!~』のページで詳しく解説しています。解き方が分からない方は、まず、そちらのページを一読してください。
設問1の解答と解説:
設問1で出てくるキーワードは、「夏が好き」「水泳が得意」の2つだけ。よって、ベン図は、「夏が好き」「水泳が得意」の2つのカテゴリに分けます。
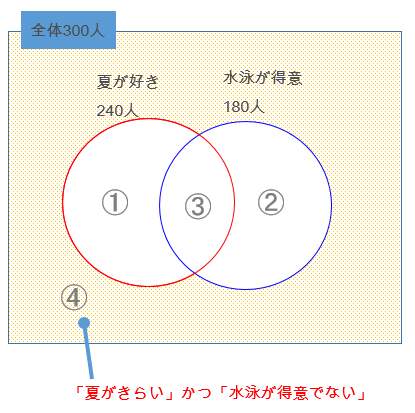
求めるのは、「夏がきらい」かつ「水泳も得意でない」人なので④の部分になります。対象人数が全員で300人なので④を求める為には、
④=300人-①-②-③
となります。
そして、設問の前提条件と、設問1の情報より下記の事がわかります。
(夏が好き)かつ(水泳が得意):
③=150人
(夏だけが好き):
①=240-③
=240-150
=90人
(水泳だけが得意):
②=180-③
=180-150
=30人
なので、よって求める解答
(夏がきらい)&(水泳が得意でない):
④=300-①-②-③
=300-90-30-150
=30人
解答:B
設問2の解答と解説:
「夏が好き」と「冬が好き」の2つのベン図を作ります。求めるのは、夏もしくは冬のどちらか一方だけが好きな人なので①と②の合計になります。
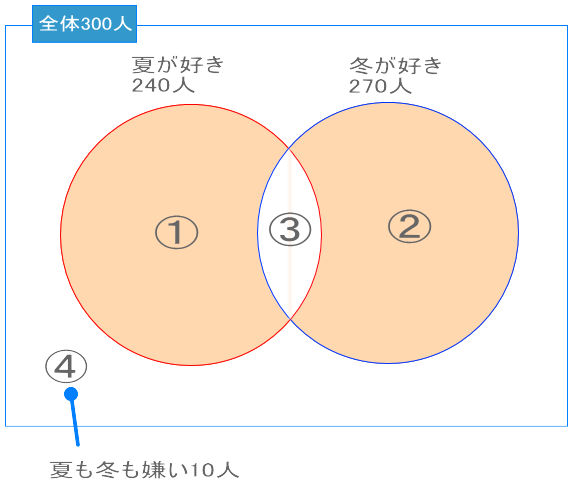
① = 240 - ③ ・・・(1)
② = 270 - ③ ・・・(2)
300 = ① + ② + ③ + ④ ・・・(3)
(1)と(2)の式より下記の式が作れます
① + ② = 510 - ③ - ③ ・・・(4)
更に求めたい、(3)の式より
① + ② = 300 - ③ - ④ = 300 - ③ - 10 = 290 - ③ ・・・(5)
ができます。(5)の式を置き換えると
- ③ = ① + ② - 290
これを(4)の式に代入すると
① + ② = 510 + ① + ② - 290 + ① + ② - 290
となる。この式を計算すると、
① + ② + ① + ② - ① - ② = 290 + 290 - 510
① + ② = 70
となる。
解答:C
どうでしょう?計算がややこしいと感じたでしょうか?もし、ややこしいと感じた方は、ベン図の考え方を変えることでもう少し計算を楽にすることはできます。むしろ、次に書く別解の方が早く正しい解き方かもしれない。
別解:
先程の解き方は、夏もしくは冬が好きな人に焦点を合わせ、それ以外の人が嫌いな人になるという考え方でしたが、今度は、夏もしくは、冬が嫌いな人に焦点を合わせたベン図をつくります。
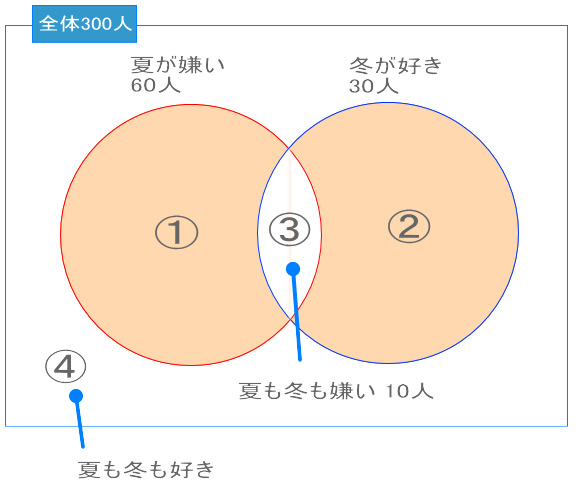
求めるのは、夏と冬のどちらか一方だけが好きな人になります。そして該当する部分は①と②というのが分かるでしょうか?①は、「夏だけが嫌い」な人です。「夏だけが嫌い」を言い換えると「冬だけが好き」になります。同様に「冬だけが嫌い」というのは、「夏だけが好き」ということになります。
よって、②は、「夏だけが好きな人」。①は、「冬だけが好きな人」。となり求める解答は、①+②となります。
① = 60 - 10 = 50
② = 30 - 10 = 20
よって解答は、
① + ② = 50 + 20 = 70人となります。
設問3の解答と解説:
求める解答は、水泳かスキーのどちらか1つでも得意な人ということは、「水泳とスキーの両方が得意でない」人以外全員のことになります。ベン図にすると下図の通りです。
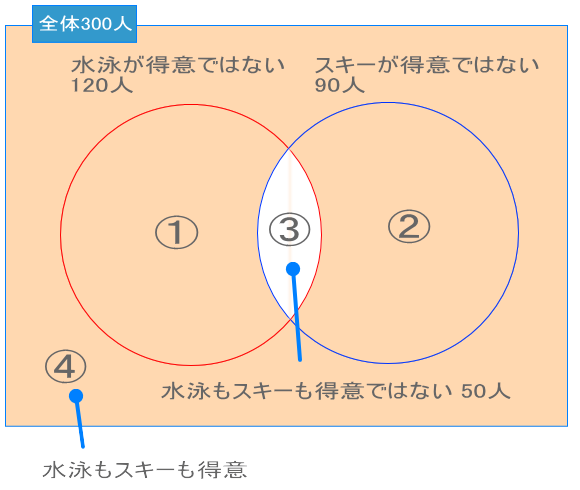
解答は、①②④の合計だが、ここは全体300人から③を引けばいいだけ。よって、
水泳かスキーのどちらか1つでも得意な人 = 300 - 50 = 250人
解答:D




設問1の問題の④には「夏が好き」で「泳げない」人も含まれていませんか?
まかない様
コメントありがとうございます。
返答遅くなり申し訳ございません。
「夏が好き」で「泳げない」人は①になります。
宜しくお願い致します。
例題3
「水泳かスキーのどちらか1つでも得意な人」=水泳とスキーが得意な人のベン図の①と②の和、とは等しくないのでしょうか…。どうしても腑に落ちなくて…。
さいたま様
コメントありがとうございます。
その考えで正しいです。解説に記載したベン図は、「得意でない人」を主眼に置いたベン図で解説していますが、「得意である人」を主眼に置いたベン図で、円①②を「水泳が得意な人」と「スキーが得意な人」にした場合は、さいたま様が言うような考えになります。