分割払いの問題について

あさかさん、ご質問ありがとうございます。質問頂いた内容を下記に解答致します。
不明な点があれば、同様に質問ページから再度ご連絡ください。記事のコメント欄に記載して頂いても結構です。

ある人がカメラを分割払いで購入することにした。購入時にいくらか頭金を払い、総額から頭金を差し引いた残額を6回の分割払いにする。このとき、分割手数料として残額の1/10を加える。

[設問１]頭金として購入価格の1/5を払った。このとき、分割払いの1回の支払額は購入価格のどれだけにあたるか？

[設問２]分割払いの1回の支払額が購入価格の1/6になるようにすると、頭金として支払うのは購入価格のどれだけにあたるか？

解答と解説

ポイント：
問題を解く過程で、『4/5 x（1 + 1/10）』という計算式が出てきます。ここで、「ん？何故、カメラの購入価格1に手数料の1/10を加え更にそれを4/5するの？」と思ってしまう。それは、この計算式『4/5 x（1 + 1/10）』の中で出てくる『1』をカメラの購入価格1として考えてしまうからです。

しかし、実はこの1は、カメラの購入価格1とは別物なのです。なので、カメラの購入価格1に手数料の1/10を加えているというわけではありません。

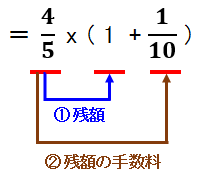
頭金を差し引いて支払わなければならない金額は、『①残額』と、『②残額の手数料』だという程度で考えればよい。参考書の解答に記載されている上記のような（　）のくくり方が誤解を招いている。私であれば、上記の（　）のくくり方ではなく、下記の様に記載する。これは（　）のくくり方の違いだけで内容は全く同じです。

設問１の解説：
　●カメラの購入価格を１とします。
　●頭金の1/5を払い、残額は4/5。
　●分割手数料は、残額の1/10なので、（4/5）ｘ（1/10）

分割払いをしなければならない価格は、頭金を差し引いた残額4/5に手数料を加えたもの。これを分割払いしてやる必要があります。それは次の式で表されます。

　分割払いをする価格 ＝ 残額 ＋ 分割手数料
　　　　　　　　　　 ＝4/5 ＋（4/5）ｘ（1/10）
　　　　　　　　　　 ＝4/5 x（1 + 1/10）・・・※１

更に求めたいのは、分割払いの1回の支払額が購入価格のどれだけにあたるかなので、分割払いをする価格を分割回数6で割ってやればよい。

　分割払い1回の支払額 ＝ 4/5 x（1 + 1/10）÷ 6 ＝ 11/75 ・・・（１）

この式（１）が解答に記載されている解答になります。

では、あさかさんの間違っていたところ

①総額を1とする。
②まず頭金の1/5を払い、残額はは4/5。
③手数料は「残額の1/10を加える」ですから、4/5×1/10 ・・・（A）
④5/4×1/6で1回分の支払額(手数料抜き) ・・・（B）
⑤A+B=購入価格の、分割払い1回の支払額

①正解
②正解
③正解
④正解
⑤5/4 ではなく、4/5ですよね？
⑥手数料が6回に分割されずに、毎回4/5×1/10の手数料が分割払いの1回の支払額に上乗せされてしまっているのが間違えている点ですね。もしこの方法でいきたいのであれば、A+Bではなく下記の様にAを6で割ってやる必要があります。

分割払い1回の支払額 = A/6+B
　　　　　　　　　　= (4/5×1/10)×1/6 + 4/5×1/6
　　　　　　　　　　= 4/300 + 4/30
　　　　　　　　　　= 4/300 + 40/300
　　　　　　　　　　= 44/300
　　　　　　　　　　= 11/75

よって、求める解答は、11/75

設問２の解説：
設問１では、頭金は購入金額の1/5でしたが、今回は不明。よって、頭金をＮとし、購入価格は設問１と同じく１とする。

購入価格：１
頭金：　Ｎ

よって、購入価格から頭金を差し引いた残額は、「１－Ｎ」となる。

購入価格から頭金を差し引いた残額： １－Ｎ ・・・（１）

更に、この「購入価格から頭金を差し引いた残額」の1/10が手数料となるので、手数料は、

分割手数料：（１－Ｎ）ｘ（１/１０） ・・・（２）

よって、（１）の残額と（２）の手数料の合計を６回に分割して支払うことになります。また、分割１回あたりの支払額が購入価格の1/6になるようにしたいので次の式が成り立ちます。

｛（１－Ｎ）＋（１－Ｎ）ｘ（１/１０）｝÷ ６ ＝ １ ｘ １/６ ・・・（３）

よって、（３）式を解けば頭金Ｎが出てきます。解く過程を下記に記載していますが、このあたりは自分のやり易いように計算して下さいね。

よって、頭金は、購入価格の１/１１となります。