SPI練習問題-問2(n進法)

SPI練習問題-問2(n進法)

ｎ進法に関する次の問題に答えなさい。

[設問１]２進数の１１１１０は１０進数であらわすといくつになるか？

[設問２]１０進数の３０は、２進数であらわすといくつになるか？

[設問３]２進数の１１１０１１は５進数であらわすといくつになるか？

解答と解説

使用する公式：
ｎ進法の解き方に関しては、『SPI ｎ進法 ～練習問題と徹底解説！～』のページで詳しく解説しているので、参考にしてください。早く解く方法なども紹介しています

設問１の解答と解説：

２進数の一桁目から２の０乗、２の１乗、２の２乗・・・と順にかけて各桁を足します。

よって、２進数１１１１０は、

　（１ｘ２⁴）＋（１ｘ２³）＋（１ｘ２²）＋（１ｘ２¹）＋（０ｘ２⁰）
＝（１ｘ１６）＋（１ｘ８）＋（１ｘ４）＋（１ｘ２）＋（０ｘ１）
＝１６＋８＋４＋２＋０
＝３０

解答：Ａ

設問２の解答と解説：

１０進数から２進数の変換は、１０進数の数を２で割った時の商が０もしくは１になるまで割り続け、その時の最後の商、さらに余りの数を下から順に並べた数が２進数の値になります。よって、１０進数の３０を２進数に変換すると次の通りになる。

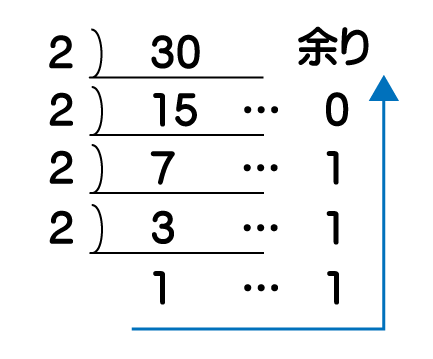
よって、求める解答は、１１１１０となります。

解答：Ｃ

設問３の解答と解説：

ｎ進数からｎ進数へ変換する問題になります。解き方は、一旦１０進数に変換し、その後、５進数に変換します。。

まずは、２進数１１１０１１を１０進数に変換します。

　（１ｘ２⁵）＋（１ｘ２⁴）＋（１ｘ２³）＋（０ｘ２²）＋（１ｘ２¹）＋（１ｘ２⁰）
＝（１ｘ３２）＋（１ｘ１６）＋（１ｘ８）＋（０ｘ４）＋（１ｘ２）＋（１ｘ１）
＝３２＋１６＋８＋０＋２＋１
＝５９

この１０進数５９を５進数に変換します。

よって、求める解答は２１４なので、Ｂとなります。

解答：Ｂ