SPI練習問題-問2(条件と領域)

SPI練習問題-問2(条件と領域)

ある工場で、原材料ＸとＹを次のような条件で仕入れることにした。

条件ａ：Ｘは、40㎏以上とする
条件ｂ：Ｘは、80㎏以下とする
条件ｃ：Ｙの重さはＸの50％以上とする
条件ｄ：Ｙの重さはＸの150％以下とする
条件ｅ：ＸとＹは合計で140㎏以下とする

Ｘを横軸、Ｙを縦軸にとって図示すると、上記の５つの条件を満たす組み合わせは下図の点ア、イ、ウ、エ、オで囲まれた領域で示される。

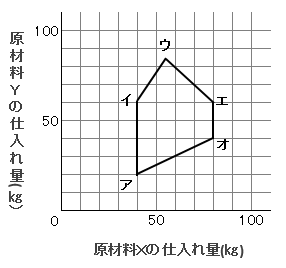
[設問１]この領域において、点アと点オを通る直線で示される境界はどの条件によるものか？

[設問２]原材料ＸとＹを合計で90㎏仕入れたい。原材料Ｘが10㎏で1000円、原材料Ｙが10㎏で5000円のとき、条件内で最も安い仕入れ値はいくらになるか？

解答と解説

『条件と領域』の問題の解き方や、使う公式に関しては『SPI 条件と領域 ～練習問題と解き方を徹底解説！～』のページで詳しく解説しています。解き方が分からない方は、まず、そちらのページを一読してください。

設問１の解答と解説：

条件ａ～ｅが線分アイ、イウ、ウエ、エオ、オアのどれに該当するかを確認する。

条件ａ
「Ｘは40㎏以上とする」という条件からＸ＝40の線分アイだということがわかる。
条件ａは、線分アイ

条件ｂ
「Ｘは80㎏以下とする」という条件からＸ＝80の線分エオだということがわかる。
条件ｂは、線分エオ

条件ｃ
「Ｙの重さはＸの50％以上とする」という条件からＹ≧Ｘ/2だということがわかる。図より、Ｘ軸方向に2移動したときＹ軸方向に1移動する線分は線分オアになる。
条件ｃは、線分オア

条件ｄ
「Ｙの重さはＸの150％以下とする」という条件からＹ≦3Ｘ/2だということがわかる。3/2が正の値なのでグラフの傾きが右上がりのグラフだということがわかる。右上がりのグラフになるのは、線分イウか線分オアしかない。ウの座標が明確ではないので、傾きが3/2のグラフかは断定できないが、線分はオアは条件ｃよりＹ＝Ｘ/2と分かっている。よって、消去法からも線分イウが条件ｄに該当することがわかる。
条件ｄは、線分イウ

条件ｅ
「ＸとＹは合計で140㎏以下とする」という条件より、Ｘ＋Ｙ≦140 ということになる。このことより、Ｙ≦ －Ｘ＋140 というグラフになることが分かる。また、傾きが－１なので右下がりのグラフになる。右下がりのグラフは、線分ウエしかないのですぐにわかる。
条件ｅは、線分ウエ

よって、設問の点アと点オを通る直線は線分オアのことなので、条件ｃが該当する。

解答：Ｃ

設問２の解答と解説：

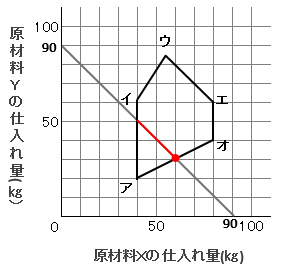原材料ＸとＹの合計を90㎏にしたいということは、次の式が成り立つ。

　Ｘ＋Ｙ＝90
　Ｙ＝－Ｘ＋90

この式のグラフは、右図のＸ座標(90, 0)とＹ座標(0, 90)を結んだ線になる。更にその領域を満たす範囲は赤線部分になる。


原材料は、Ｘが10㎏で1000円、Ｙが10㎏で5000円なので、最も安く仕入れる為には、Ｙが一番小さい値を取る点になる。その点は、線分オアと交わる座標(60, 30)の点である。

よって、仕入れ値の合計は、

　Ｘが60㎏なので、1000円ｘ6＝6000円
　Ｙが30㎏なので、5000円ｘ3＝15000円

　合計21000円のＤとなる。

解答：Ｄ

※解説内容で不明な点があれば、質問フォームから問い合わせして下さい。どんな些細な質問でも結構です。