SPI練習問題-問1(条件と領域)
あるスポーツクラブでは、ストレッチ、筋力トレーニング、エアロビクス、の3種目を、以下に示す条件を満たすように選択しなければならない。なお、1時間を単位として行う。
a 全部で24時間選択
b ストレッチは3時間以上選択
c 筋力トレーニングは4時間以上選択
d エアロビクスは7時間以上選択
e ストレッチは10時間以下で選択
下の図は、上の5つの条件を満たす領域を図に示した。
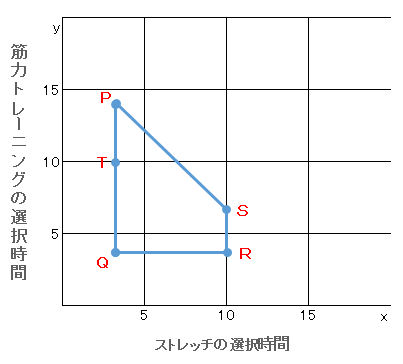
[設問1]点Qと点Rを通る直線で表される境界は、上のどの条件によるものか?
A aのみ
B bのみ
C cのみ
D dのみ
E eのみ
F aとb
G aとc
H aとd
I aとえ
J bとc
K いずれでもない
[設問2]点Pと点Sを通る直線で表される境界は、上のどの条件によるものか?
A aのみ
B bのみ
C cのみ
D dのみ
E eのみ
F aとb
G aとc
H aとd
I aとえ
J bとc
K いずれでもない
[設問3]点P、点Q、点R、点Sのうち、点Tと比べてエアロビクスの選択時間が多くなるのはどの点か?
A 点Pのみ
B 点Qのみ
C 点Rのみ
D 点Sのみ
E 点Pと点Q
F 点Pと点S
G 点Qと点R
H 点Sと点R
I いずれでもない
解答と解説
『条件と領域』の問題の解き方や、使う公式に関しては『SPI 条件と領域 ~練習問題と解き方を徹底解説!~』のページで詳しく解説しています。解き方が分からない方は、まず、そちらのページを一読してください。
前提条件の確認:
前提条件a~eを式になおしてみる。これをしておくことで問題は解きやすくなります。
a 全部で24時間選択
筋力トレーニング時間:y
ストレッチ時間:x
エアロビクス時間:z
とすると、x + y + z = 24
b ストレッチは3時間以上選択
x ≧ 3
c 筋力トレーニングは4時間以上選択
y ≧ 4
d エアロビクスは7時間以上選択
z ≧ 7
e ストレッチは10時間以下で選択
x ≦ 10
設問1の解答と解説:
直線QRは、y軸(筋力トレーニングの選択時間)を式になおすと、y = a となる。前提条件の確認で作った式に含まれるのはc。よって、求める解答はC。
解答:C
設問2の解答と解説:
直線PSは右下がりのグラフなので、y = -ax + c という式になることがわかります。。前提条件の確認で作った式と一致するのは、a。
y = -x + 24 - z
ここで、zというのは仮に置いた文字でグラフ上では存在しません。よって、dのz ≧ 7をこの式に代入します。
y = -x + 17
よって、線PSは上記の式で表すことができます。条件としてはdも関わることになるので解答としては、aとdが正解となります。少し難しいですね。線分PSは、筋力トレーニングの時間と、ストレッチの時間、この2つ時間のみの合計と言う点に気付かないと解くのは少し難しい。
解答:H
設問3の解答と解説:
エアロビクスの時間を多くするためには、筋力トレーニングとストレッチの選択時間を減らす必要があります。
点T点は、
ストレッチの選択最小時間:3時間
筋力トレーニングの選択:10時間
よって、T点座標は(3, 10)
合計13時間になります。エアロビクスの時間をこれよりも多くするためには、13時間以下にする必要があります。そして、もう1点筋力トレーニングとストレッチの選択時間合計が13時間になるポイントがあるのが分かりますでしょうか?
T点は、ストレッチが最小時間を取った取った時のポイント。もう一つのポイントは、筋力トレーニングが最小時間を取った時のポイントです。筋力トレーニングは、4時間以上取る必要があるので、最小は4時間になります。
よって、もうひとつのポイントをZとすると
ストレッチの選択時間:9時間
筋力トレーニングの選択最小時間:4時間
Z点座標は(9, 4)
この2点を線で結ぶと下表のようになります。
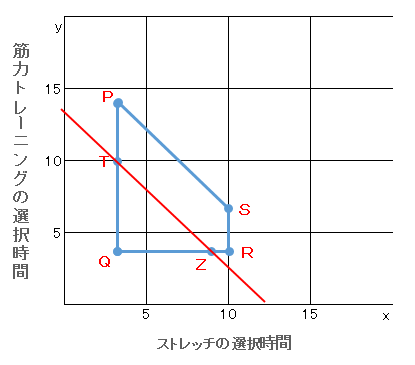
この赤ラインより下側が筋力トレーニングとストレッチの選択時間が少なくなるポイントです。このポイントにあるのは点Qだけなので、求める解答はBとなります。
解答:B



