SPI練習問題-問4(ブラックボックス)

SPI練習問題-問4(ブラックボックス)

入力信号０、１を次のように変換する装置Ｐ、Ｑ、Ｒがある。

（１）Ｐは、同時に入力された２つの信号が同じ数ならば０を、違う数ならば１を出力する。
（２）Ｑは、同時に入力された２つの信号の内、少なくとも一方が０の場合には０を、２つとも１の場合には１を出力する。
（３）Ｒは、同時に入力された２つの信号の内、少なくとも一方が１の場合には３/４の確率で１を出力し、１/４の確率で０を出力する。また２つもと０の場合には０を出力する。

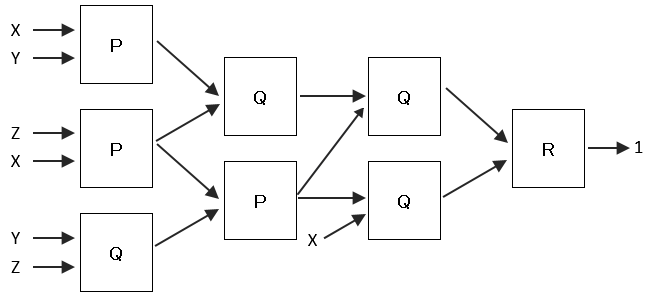
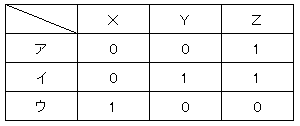
[設問１]この装置を次の図の様に接続してＸ、Ｙ、Ｚを入力したところ、最終的には１が出力された。Ｘ、Ｙ、Ｚに当てはまる組み合わせはア～ウのうちどれか？

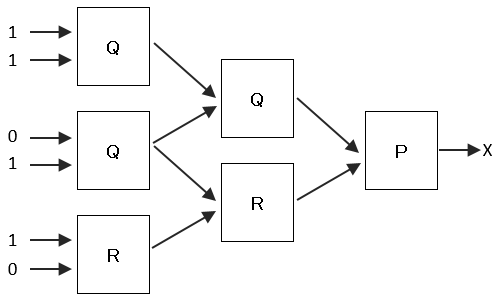
[設問２]このＰ、Ｑ、Ｒを次の図の様に接続しなおした。最終的に出力されるＸが１になる確率はいくらか？

[設問３]このＰ、Ｑ、Ｒを次のように接続しなおしたところ、最終的に出力されたＹは１であった。このことに必ずしも矛盾しないのは、次のア～ウのうちどれか？

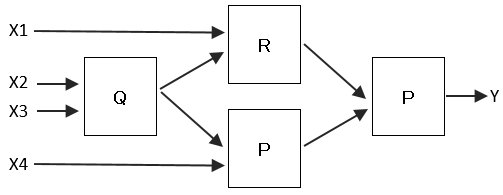
ア　入力X1、X2、X3、X4は、すべて０である。
イ　入力X1、X2、X3、X4は、すべて１である。
ウ　入力X1、X4は０であり、X2、X3のいずれか１つが１である。

解答と解説

設問１の解答と解説：

最終的な出力１の方から求めていくこともかのうですが、ここは素直にア、イ、ウのの３パターンを順番に入力し確認する方が確実で早い。

ア　Ｘ＝０、Ｙ＝０、Ｚ＝１の場合
順番に各装置の出力を求めていくと、最後の装置Ｒへの入力は、２入力とも０となる。入力が２つもの０の場合は、Ｒの出力も０となるため、結果が異なる。よって、アの組み合わせは誤り。

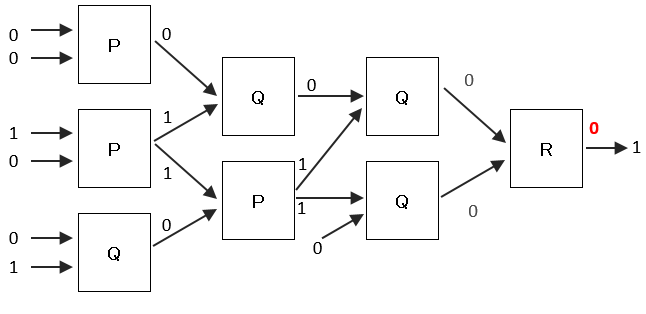
イ　Ｘ＝０、Ｙ＝１、Ｚ＝１の場合
順番に各装置の出力を求めていくと、最後の装置Ｒへの入力は、２入力とも０となる。入力が２つもの０の場合は、Ｒの出力も０となるため、結果が異なる。よって、イの組み合わせは誤り。

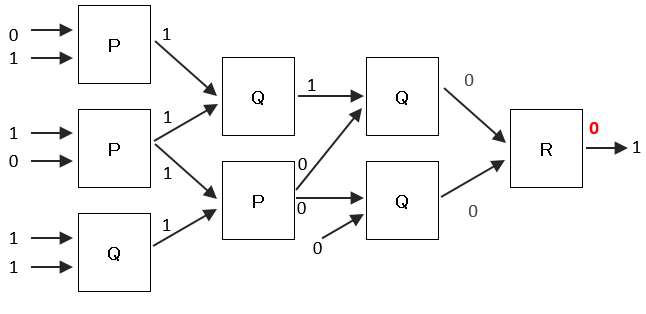
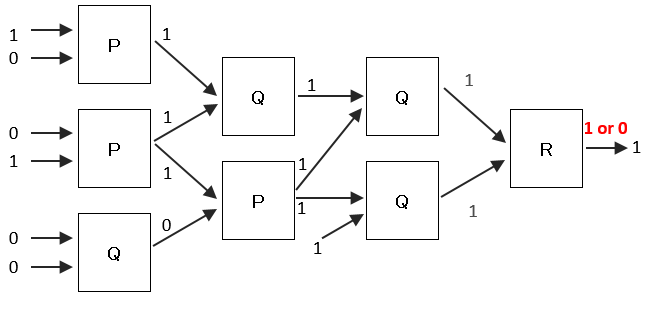
ウ　Ｘ＝１、Ｙ＝０、Ｚ＝０の場合
順番に各装置の出力を求めていくと、最後の装置Ｒへの入力は、２入力とも１となる。２入力の内、どちらか一方が１の場合は、４分の３の確率で１を出力し、４分の１の確率で０を出力するということなので、０と１両方を取りうる可能性があります。よって、ウの組み合わせは正解。

求める解答は、ウだけなのでＣが解答となります。

解答：Ｃ

設問２の解答と解説：

最後の装置Ｐの入力の１つ③は、「0」となる。よって、Ｘが１となるためには、もう１つの入力値②は１を取ることが必須になるのだが、最初の装置Ｒの出力①が１となるのは３/４の確率になる。また、３/４の確率で１が出力されたとしても、次の装置Ｒでも出力②が１となるためには更に３/４の確率になる。

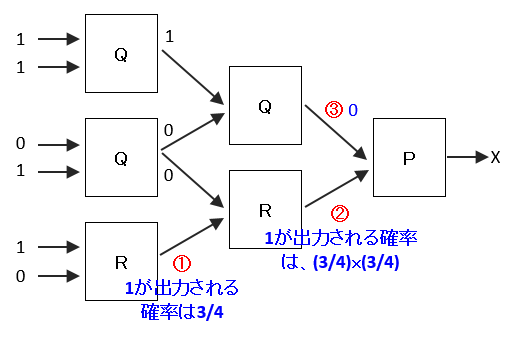
「装置Ｐの出力が１になる確率」＝「装置Ｐの入力②が１になる確率」の式が成り立ちます。

装置Ｐの入力②が１になる確率は、（３/４）ｘ（３/４）＝９/１６となります。

よって、求める解答は、９/１６でＤが正解になります。

解答：Ｄ

設問３の解答と解説：

設問１と同じようにア、イ、ウの３つの入力パターンを実際に入力し、確認していきます。

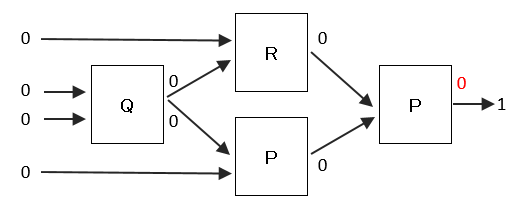
ア　Ｘ１＝０、Ｘ２＝０、Ｘ３＝０、Ｘ４＝０の場合
順番に各装置の出力を求めていくと、最後の装置Ｐの出力は、０となり矛盾が発生するので誤り。

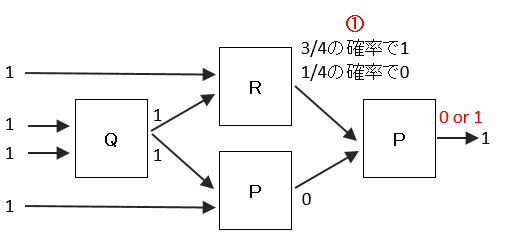
イ　Ｘ１＝１、Ｘ２＝１、Ｘ３＝１、Ｘ４＝１の場合
順番に各装置の出力を求めていくと、装置Ｒの出力は、確率次第で０も１も取りうる値になります。よって、最後の装置Ｐの出力も確率次第で０でも１でも取りうることになるので、必ずしも矛盾するとは言えない。よって、イの組み合わせは正しい。

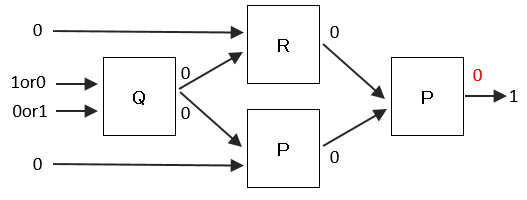
ウ　Ｘ１＝０、Ｘ４＝０、Ｘ２かＸ３のいずれかが１の場合
最初の装置Ｑの２つの入力値の一方は、少なくとも０となるので、出力は０が決定する。よって、各装置の出力を求めていくと最後の装置Ｐの出力は０となることが分かる。よって、矛盾した結果となるので誤り。

求める解答は、イだけが矛盾しないのでＢが解答となります。

解答：Ｂ